题目内容
2.若A={x|x=4k+1,k∈Z},B={x|x=2k-1,k∈Z},则( )| A. | A⊆B | B. | B⊆A | C. | A=B | D. | A∩B=∅ |
分析 由整数的整除性,可得A表示除以4余1的整数,B表示奇数集.由此利用集合的关系,不难得到本题的答案.
解答 解:∵集合B={x|x=2k-1,k∈z},A={x|x=4k+1,k∈Z},
∴B表示奇数集,A表示除以4余1的整数,
∴B?A.
故选:A.
点评 本题考查集合的包含关系,考查学生分析解决问题的能力,关键是对集合含义的理解.

练习册系列答案
相关题目
13.下列函数为奇函数的是( )
| A. | y=|x| | B. | y=3-x | C. | y=$\frac{1}{{x}^{3}}$ | D. | y=-x2+14 |
10.在(x2+$\frac{1}{x}$)10的展开式中,系数最大项为( )
| A. | 第5项 | B. | 第6项 | C. | 第7项 | D. | 第5项或第6项 |
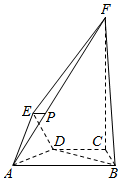 如图几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,CB=CD=2.面EAD⊥面ABCD,面FCB⊥面ABCD,且CF⊥BC.
如图几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,CB=CD=2.面EAD⊥面ABCD,面FCB⊥面ABCD,且CF⊥BC.