题目内容
2.已知函数f(x)的定义域为R,且f(x)=$\left\{\begin{array}{l}{{x}^{2}+2,x∈[0,1]}\\{2-{x}^{2},x∈(-1,0)}\end{array}\right.$,f(x+1)=f(x-1),则方程f(x)=$\frac{2x+1}{x}$在区间[3,-3]上的所有实根之和为( )| A. | -8 | B. | -2 | C. | 1 | D. | 8 |
分析 可判断函数f(x)的周期为2,从而化简可得f(x)-2=$\frac{1}{x}$,作函数f(x)-2与y=$\frac{1}{x}$在[-3,3]上的图象,从而结合图象解得.
解答  解:∵f(x+1)=f(x-1),
解:∵f(x+1)=f(x-1),
∴函数f(x)的周期为2,
∵f(x)=$\frac{2x+1}{x}$,
∴f(x)-2=$\frac{1}{x}$,
∵f(x)=$\left\{\begin{array}{l}{{x}^{2}+2,x∈[0,1]}\\{2-{x}^{2},x∈(-1,0)}\end{array}\right.$,
∴f(x)-2=$\left\{\begin{array}{l}{{x}^{2},x∈[0,1]}\\{-{x}^{2},x∈(-1,0)}\end{array}\right.$,
作函数f(x)-2与y=$\frac{1}{x}$在[-3,3]上的图象如下,
易知点A与点C关于原点对称,
故方程f(x)=$\frac{2x+1}{x}$在区间[3,-3]上的所有实根之和为1,
故选C.
点评 本题考查了数形结合的思想应用及方程与函数的关系应用.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
16.在△ABC中,BC=1,ccosA+acosC=2bcosB,△ABC的面积S=$\sqrt{3}$,则AC等于( )
| A. | $\sqrt{13}$ | B. | 4 | C. | 3 | D. | $\sqrt{15}$ |
14.已知f(x)=2sin(ωx+$\frac{π}{4}$),x∈R,其中ω是正实数,若函数f(x)图象上一个最高点与其相邻的一个最低点的距离为5,则ω的值是( )
| A. | $\frac{2π}{5}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{5}$ | D. | $\frac{π}{3}$ |
7.已知数列{an}是等差数列,数列{bn}是等比数列,公比为q,数列{cn}中,cn=anbn,Sn是数列{cn}前n项和,若Sm=11,S2m=7,S3m=-201(m为正偶数),则S4m的值为( )
| A. | -1601 | B. | -1801 | C. | -2001 | D. | -2201 |
11.已知集合A={x|y=$\sqrt{x-{x^2}}$),B={y|y-l<0),则A∩B=( )
| A. | (一∞,1) | B. | (一∞,1] | C. | [0,1) | D. | [0,1] |
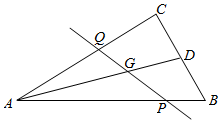 如图,过△ABC的重心G的直线分别交边AB、AC于P、Q两点,且$\overrightarrow{AB}$=x$\overrightarrow{AP}$,$\overrightarrow{AC}$=y$\overrightarrow{AQ}$,则xy的取值范围是[2,$\frac{9}{4}$].
如图,过△ABC的重心G的直线分别交边AB、AC于P、Q两点,且$\overrightarrow{AB}$=x$\overrightarrow{AP}$,$\overrightarrow{AC}$=y$\overrightarrow{AQ}$,则xy的取值范围是[2,$\frac{9}{4}$].