题目内容
3.已知正实数m,若x10=a0+a1(m-x)+a2(m-x)2+…+a10(m-x)10,其中a8=180,则m值为( )| A. | 4 | B. | 2 | C. | 3 | D. | 6 |
分析 根据题意,x10=[m-(m-x)]10,利用二项式展开式定理求出展开式的第8项系数,列出方程求出m的值.
解答 解:∵x10=a0+a1(m-x)+a2(m-x)2+…+a10(m-x)10,
且x10=[m-(m-x)]10
=${C}_{10}^{0}$•m10-${C}_{10}^{1}$•m9•(m-x)+${C}_{10}^{2}$•m8•(m-x)2-…+${C}_{10}^{8}$•m2•(m-x)8-${C}_{10}^{9}$•m•(m-x)9+${C}_{10}^{10}$•(m-x)10
=a0+a1(x-1)+a2(x-1)2+…+a10(x-1)10,
∴a8=${C}_{10}^{8}$m2=180,
即45m2=180,
解得m=2或m=-2(不合题意,舍去),
∴m的值为2.
故选:B.
点评 本题考查了二项式定理展开式中系数的求法以及二项式特定项的求法问题,是基础题目.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
11.已知集合A={x|y=$\sqrt{x-{x^2}}$),B={y|y-l<0),则A∩B=( )
| A. | (一∞,1) | B. | (一∞,1] | C. | [0,1) | D. | [0,1] |
18.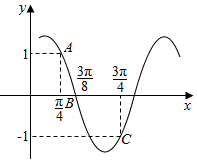 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若tanα=3,则f($α+\frac{π}{8}$)的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若tanα=3,则f($α+\frac{π}{8}$)的值为( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若tanα=3,则f($α+\frac{π}{8}$)的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若tanα=3,则f($α+\frac{π}{8}$)的值为( )| A. | -$\frac{3}{5}$ | B. | -$\frac{4}{5}$ | C. | -$\frac{3\sqrt{2}}{5}$ | D. | -$\frac{4\sqrt{2}}{5}$ |
8.已知x,y是实数,则“$\left\{\begin{array}{l}{x>1}\\{y>1}\end{array}\right.$”是$\left\{\begin{array}{l}{x+y>2}\\{xy>1}\end{array}\right.$的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
13.下列函数为奇函数的是( )
| A. | y=|x| | B. | y=3-x | C. | y=$\frac{1}{{x}^{3}}$ | D. | y=-x2+14 |
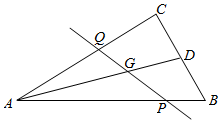 如图,过△ABC的重心G的直线分别交边AB、AC于P、Q两点,且$\overrightarrow{AB}$=x$\overrightarrow{AP}$,$\overrightarrow{AC}$=y$\overrightarrow{AQ}$,则xy的取值范围是[2,$\frac{9}{4}$].
如图,过△ABC的重心G的直线分别交边AB、AC于P、Q两点,且$\overrightarrow{AB}$=x$\overrightarrow{AP}$,$\overrightarrow{AC}$=y$\overrightarrow{AQ}$,则xy的取值范围是[2,$\frac{9}{4}$]. 已知正三角形A1A2A3,A4、A5、A6分别是所在棱的中点,如图,则当1≤i≤6,1≤j≤6,且i≠j时,数量积$\overrightarrow{{A}_{1}{A}_{2}}$•$\overrightarrow{{A}_{i}{A}_{j}}$的不同数量积的个数为9.
已知正三角形A1A2A3,A4、A5、A6分别是所在棱的中点,如图,则当1≤i≤6,1≤j≤6,且i≠j时,数量积$\overrightarrow{{A}_{1}{A}_{2}}$•$\overrightarrow{{A}_{i}{A}_{j}}$的不同数量积的个数为9.