题目内容
已知|| OA |
| OB |
| OA |
| OB |
| OC |
| OA |
| OC |
| OC |
| OA |
| OB |
考点：向量在几何中的应用
专题：平面向量及应用
分析：以O为原点建立直角坐标系，求出
、
、
向量，利用
=m
+n
列出方程组，即可求出m，n的值．
| OA |
| OB |
| OC |
| OC |
| OA |
| OB |
解答：
解：如图所示建立直角坐标系，则
=（1，0），
=(-
，
)，
=(
，
)，
由于
=m
+n
，
所以有：
，解之
．
故答案为：m=5，n-5．
解：如图所示建立直角坐标系，则| OA |
| OB |
| 1 |
| 2 |
| ||
| 2 |
| OC |
| 5 |
| 2 |
5
| ||
| 2 |
由于
| OC |
| OA |
| OB |
所以有：
|
|
故答案为：m=5，n-5．
点评：本题考查向量在几何中的应用，正确建立坐标系能够使解答运算简便．
练习册系列答案
相关题目
设全集U=R，A={x|x≤1+
，x∈R }，B={1，2，3，4}，则B∩∁UA=（ ）
| 2 |
| A、{4} |
| B、{3，4} |
| C、{2，3，4} |
| D、{1，2，3，4} |
命题“?x∈R，sinx＞-1”的否定是（ ）
| A、?x∈R，sinx≤-1 |
| B、?x0∈R，sinx0≤-1 |
| C、?x0∈R，sinx0＞-1 |
| D、不存在x∈R，sinx＞-1 |
设M是△ABC所在平面上的一点，且
+
+
=
，D是AC中点，则
的值为（ ）
| MB |
| 3 |
| 2 |
| MA |
| 3 |
| 2 |
| MC |
| 0 |
|
| ||
| |BM| |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
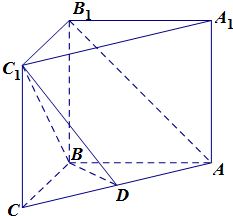如图，在三棱柱ABC-A1B1C1中，侧棱A1A⊥底面ABC，∠ABC=
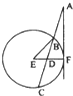如图，过圆E外一点A作一条直线与圆E交与B，且AB=