题目内容
函数y=
的定义域为 ．
| ||
| x-1 |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：由式子有意义需使分母和根号有意义，可得x的范围，写成集合的形式可得函数的定义域．
解答：
解：要使函数的表达式有意义，x须满足：
⇒
，
即x∈[-2，1）∪（1，2]，
故定义域为：[-2，1）∪（1，2]，
故答案为：[-2，1）∪（1，2]，
|
|
即x∈[-2，1）∪（1，2]，
故定义域为：[-2，1）∪（1，2]，
故答案为：[-2，1）∪（1，2]，
点评：本题考查了函数的定义域问题，注意分母和根号的特点，本题属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
设全集U=R，A={x|x≤1+
，x∈R }，B={1，2，3，4}，则B∩∁UA=（ ）
| 2 |
| A、{4} |
| B、{3，4} |
| C、{2，3，4} |
| D、{1，2，3，4} |
命题“?x∈R，sinx＞-1”的否定是（ ）
| A、?x∈R，sinx≤-1 |
| B、?x0∈R，sinx0≤-1 |
| C、?x0∈R，sinx0＞-1 |
| D、不存在x∈R，sinx＞-1 |
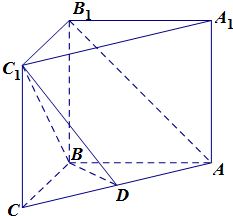如图，在三棱柱ABC-A1B1C1中，侧棱A1A⊥底面ABC，∠ABC=