题目内容
解关于x的方程:
=15.
| 1-x4 |
| x3(1-x) |
考点:根的存在性及根的个数判断
专题:计算题
分析:方程两边同乘x3(1-x)将方程化为整式方程,进而利用因式分解法,解方程,检验后,可得原方程的根.
解答:
解:方程两边同乘x3(1-x)得:
1-x4=15[x3(1-x)],
即14x4-15x3+1=0,
(x-1)(14x3-x2-x-1)=0,
(x-1)(2x-1)(7x2+3x+1)=0,
解得x=1,或x=
,
将x=1代入x3(1-x)=0,故x=1为增根,
将x=
代入x3(1-x)≠0,故x=
是原方程的根,
故方程:
=15的根为
.
1-x4=15[x3(1-x)],
即14x4-15x3+1=0,
(x-1)(14x3-x2-x-1)=0,
(x-1)(2x-1)(7x2+3x+1)=0,
解得x=1,或x=
| 1 |
| 2 |
将x=1代入x3(1-x)=0,故x=1为增根,
将x=
| 1 |
| 2 |
| 1 |
| 2 |
故方程:
| 1-x4 |
| x3(1-x) |
| 1 |
| 2 |
点评:本题考查的知识点是根的存在性,解方程,将方式方程转化为整式方程是解答的关键,但高次方程的解答难度较大.

练习册系列答案
相关题目
“(2x+1)x=0”是“x=0”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
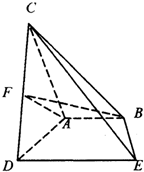 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.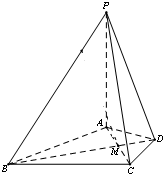 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°.
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°.