题目内容
6.甲乙两家快递公司,其快递员的日工资方案如下:甲公司底薪70元,每单抽成2;乙公式无底薪,40单内(含40单)的部分每单抽成4元,超出40单的部分每单抽成6元,假设同一公司快递员一天送快递单数相同,现从两家公司各随机抽取一名快递员,并分别记录其100天的送快递单数,得到如下的频率表:甲公司快递员送快递单数频数表
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 20 | 40 | 20 | 10 | 10 |
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 10 | 20 | 20 | 40 | 10 |
(2)小明到甲乙两家公司中的一家应聘快递员,如果仅从日工资的角度考虑,请利用所学的统计学知识为他作出选择,并说明理由.
分析 (1)设乙公司快递员送快递单数为a,由a的不同取值求出相应在的X,得到X的所有可能取值为152,156,160,166,172,由此能求出X的分布列和E(X).
(2)依题意,能求出甲公司快递员日平均快递单数,从而能求出甲公司送餐员日平均工资,再求出乙公司送餐员日平均工资,由此推荐小明去乙公司应聃.
解答 解:(1)设乙公司快递员送快递单数为a,
当a=38时,X=38×4=152,
当a=39时,X=39×4=156,
当a=40时,X=40×4=160,
当a=41时,X=40×4+1×6=166,
当a=42时,X=40×4+2×6=172,
∴X的所有可能取值为152,156,160,166,172,
∴X的分布列为:
| X | 152 | 156 | 160 | 166 | 172 |
| P | $\frac{1}{10}$ | $\frac{1}{5}$ | $\frac{1}{5}$ | $\frac{2}{5}$ | $\frac{1}{10}$ |
(2)依题意,甲公司快递员日平均快递单数为:
38×0.2+39×0.4+40×0.2+41×0.1+42×0.1=39.5.
∴甲公司送餐员日平均工资为70+2×39.5=149元,
由(1)得乙公司送餐员日平均工资为162元,
∵149<162,
∴推荐小明去乙公司应聃.
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
14.如果有95%的把握说事件A和B有关,那么具体算出的数据满足( )
| A. | K 2>3.841 | B. | K 2<3.841 | C. | K 2>6.635 | D. | K 2<6.635 |
1.已知函数f(x)=cos(2x+φ),且${∫}_{0}^{\frac{2}{3}π}$f(x)dx=0,则下列说法正确的是( )
| A. | f(x)的一条对称轴为x=$\frac{5π}{12}$ | |
| B. | 存在φ使得f(x)在区间[-$\frac{π}{6}$,$\frac{π}{3}$]上单调递减 | |
| C. | f(x)的一个对称中心为($\frac{5π}{12}$,0) | |
| D. | 存在φ使得f(x)在区间[$\frac{π}{12}$,$\frac{7π}{12}$]上单调递增 |
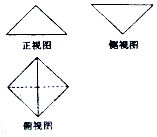 如图是一个几何体的三视图,其中正视图和侧视图是高为2,底边长为$2\sqrt{2}$的等腰三角形,俯视图是边长为2的正方形,则该几何体的外接球的体积是4$\sqrt{3}$π.
如图是一个几何体的三视图,其中正视图和侧视图是高为2,底边长为$2\sqrt{2}$的等腰三角形,俯视图是边长为2的正方形,则该几何体的外接球的体积是4$\sqrt{3}$π.