题目内容
16.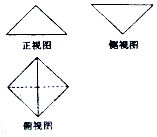 如图是一个几何体的三视图,其中正视图和侧视图是高为2,底边长为$2\sqrt{2}$的等腰三角形,俯视图是边长为2的正方形,则该几何体的外接球的体积是4$\sqrt{3}$π.
如图是一个几何体的三视图,其中正视图和侧视图是高为2,底边长为$2\sqrt{2}$的等腰三角形,俯视图是边长为2的正方形,则该几何体的外接球的体积是4$\sqrt{3}$π.
分析 由三视图可知:该几何体为四棱锥.CD=AB=2$\sqrt{2}$,AB与CD之间的距离为2.分别取AB,CD的中点E,F,取EF的中点O,为该几何体的外接球的球心.
解答 解:由三视图可知:该几何体为四棱锥.CD=AB=2$\sqrt{2}$,AB与CD之间的距离为2.
分别取AB,CD的中点E,F,取EF的中点O,为该几何体的外接球的球心.
则半径R=$\sqrt{(\sqrt{2})^{2}+{1}^{2}}$=$\sqrt{3}$.
∴该几何体的外接球的体积V=$\frac{4}{3}π×(\sqrt{3})^{3}$=4$\sqrt{3}$π.
故答案为:$4\sqrt{3}π$.
点评 本题考查了四棱锥的三视图、球的体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.甲乙两家快递公司,其快递员的日工资方案如下:甲公司底薪70元,每单抽成2;乙公式无底薪,40单内(含40单)的部分每单抽成4元,超出40单的部分每单抽成6元,假设同一公司快递员一天送快递单数相同,现从两家公司各随机抽取一名快递员,并分别记录其100天的送快递单数,得到如下的频率表:
甲公司快递员送快递单数频数表
乙公司快递员送快递单数频数表
(1)记乙公司快递员日工资为X(单位:元),求X的分布列和数学期望;
(2)小明到甲乙两家公司中的一家应聘快递员,如果仅从日工资的角度考虑,请利用所学的统计学知识为他作出选择,并说明理由.
甲公司快递员送快递单数频数表
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 20 | 40 | 20 | 10 | 10 |
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 10 | 20 | 20 | 40 | 10 |
(2)小明到甲乙两家公司中的一家应聘快递员,如果仅从日工资的角度考虑,请利用所学的统计学知识为他作出选择,并说明理由.
4.执行如图所示的程序框图,如果输入的a,b分别为56,140,则输出的a=( )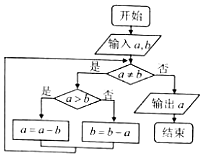

| A. | 0 | B. | 7 | C. | 14 | D. | 28 |
11.已知复数z满足1+i=(1-i)2z,则z的共轭复数在复平面内所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.如图是求12+22+32+…+1002的程序框图,则图中的①②分别是( )
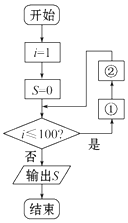

| A. | ①S=S+i ②i=i+1 | B. | ①S=S+i2 ②i=i+1 | C. | ①i=i+1 ②S=S+i | D. | ①i=i+1 ②S=S+i2 |
 一个几何体的三视图如图所示(单位:m),则该几何体的体积为15m3.
一个几何体的三视图如图所示(单位:m),则该几何体的体积为15m3.