题目内容
11.结合下面的算法:第一步,输入x
第二步,判断x是否小于0,若是则输出x+2,结束程序;否则执行第三步
第三步,输出x-1,结束程序;
当输入的x的值分别是-1,0,1时,输出的结果分别为1,-1,0.
分析 根据x值与0的关系,选择执行不同的步骤,当x的值为-1,0,1时,输出的结果应分别为1,-1,0.
解答 解:由题意,f(x)=$\left\{\begin{array}{l}{x+2,x<0}\\{x-1,x≥0}\end{array}\right.$
根据x值与0的关系,选择执行不同的步骤,当x的值为-1,0,1时,输出的结果应分别为1,-1,0,
故答案为:1,-1,0.
点评 算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.程序填空也是重要的考试题型,这种题考试的重点有:①分支的条件②循环的条件③变量的赋值④变量的输出.其中前两点考试的概率更大.此种题型的易忽略点是:不能准确理解流程图的含义而导致错误.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
1.设随机变量X~B ( n,p ),且EX=6,DX=3,则P(X=1)的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{16}$ | C. | $\frac{3}{1024}$ | D. | $\frac{1}{256}$ |
2.图(1)、图(2)、图(3)、图(4)分别包含1、5、13和25个互不重叠的单位正方形,按同样的方式构造图形,则第n个图包含( )个互不重叠的单位正方形.
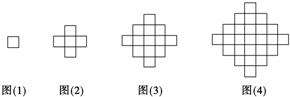

| A. | n2-2n+1 | B. | 2n2-2n+1 | C. | 2n2+2 | D. | 2n2-n+1 |
16.将曲线C按照伸缩变换$\left\{{\begin{array}{l}{x'=2x}\\{y'=3y}\end{array}}\right.$后得到的曲线方程为x'-y'+4=0,则曲线C的方程为( )
| A. | 2x+3y-4=0 | B. | 3x-2y+4=0 | C. | 2x-3y+4=0 | D. | 3x-2y+24=0 |