题目内容
1.设随机变量X~B ( n,p ),且EX=6,DX=3,则P(X=1)的值为( )| A. | $\frac{3}{4}$ | B. | $\frac{1}{16}$ | C. | $\frac{3}{1024}$ | D. | $\frac{1}{256}$ |
分析 根据随机变量符合二项分布,根据期望值求出n、p的值,写出对应的自变量的概率的计算公式,代入自变量等于1时的值.
解答 解:∵随机变量X~B ( n,p ),且EX=6,DX=3,
∴np=6,np(1-p)=3,
∴n=12,p=0.5
∴P(X=1)=C121(0.5)1(0.5)11=$\frac{3}{1024}$
故选C.
点评 本题考查二项分布,本题解题的关键是写出变量对应的概率的表示式和期望的表示式,根据期望、方差值做出n,p的值,本题是一个基础题.

练习册系列答案
相关题目
6.在极坐标系中,圆心在($\sqrt{2}$,π)且过极点的圆的方程为( )
| A. | ρ=2$\sqrt{2}$cos θ | B. | ρ=-2$\sqrt{2}$cos θ | C. | ρ=2$\sqrt{2}$sin θ | D. | ρ=-2$\sqrt{2}$sin θ |
13.若关于x的不等式|x+3|-|x-1|>a2-3a的解集不空,则实数a的范围是( )
| A. | (-∞,-1)∪(4,+∞) | B. | (-1,4) | C. | (-∞,-4)∪(1,+∞) | D. | (-4,1) |
10.有5名同学站成一排照相,则甲与乙相邻的不同排法种数有( )
| A. | 8 | B. | 12 | C. | 36 | D. | 48 |
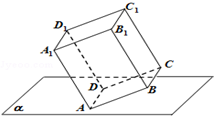 长方体ABCD-A1B1C1D1中,已知AA1=3,AB=AD=2,棱AD在平面α内,则长方体在平面α内的射影所构成的图形面积的取值范围是$4≤S≤2\sqrt{13}$.
长方体ABCD-A1B1C1D1中,已知AA1=3,AB=AD=2,棱AD在平面α内,则长方体在平面α内的射影所构成的图形面积的取值范围是$4≤S≤2\sqrt{13}$.