题目内容
6.离心率e=$\frac{1}{3}$,焦距为4的椭圆标准方程为$\frac{x^2}{36}+\frac{y^2}{32}=1$或$\frac{y^2}{36}+\frac{x^2}{32}=1$.分析 利用椭圆的离心率e=$\frac{1}{3}$,焦距为4,可得c=2,a=6,求出b,即可求出椭圆的标准方程.
解答 解:∵椭圆的离心率e=$\frac{1}{3}$,焦距为4,
∴c=2,a=6,
∴b=$\sqrt{32}$,
∴椭圆的标准方程为$\frac{x^2}{36}+\frac{y^2}{32}=1$或$\frac{y^2}{36}+\frac{x^2}{32}=1$.
故答案为:$\frac{x^2}{36}+\frac{y^2}{32}=1$或$\frac{y^2}{36}+\frac{x^2}{32}=1$.
点评 本题考查椭圆的标准方程与性质,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
相关题目
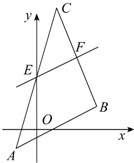 已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,且E、F分别是AC、BC的中点.求:
已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,且E、F分别是AC、BC的中点.求: