题目内容
3.(1)已知tanα=-$\frac{1}{2}$,求$\frac{1}{{{{sin}^2}α-sinαcosα-2{{cos}^2}α}}$的值;(2)求函数y=$\sqrt{2cosx-1}$的定义域.
分析 (1)由条件利用同角三角函数的基本关系,求得要求式子的值.
(2)由函数的定义域可得求得cosx≥$\frac{1}{2}$,由此求得x的范围,即为函数的定义域.
解答 解:(1)∵已知tanα=-$\frac{1}{2}$,∴$\frac{1}{{{{sin}^2}α-sinαcosα-2{{cos}^2}α}}$=$\frac{{sin}^{2}α{+cos}^{2}α}{{sin}^{2}α-sinαcosα-{2cos}^{2}α}$=$\frac{{tan}^{2}α+1}{{tan}^{2}α-tanα-2}$=-1.
(2)对于函数y=$\sqrt{2cosx-1}$,由2cosx-1≥0,求得cosx≥$\frac{1}{2}$,∴2kπ-$\frac{π}{3}$≤x≤2kπ+$\frac{π}{3}$,
故函数的定义域为{x|2kπ-$\frac{π}{3}$≤x≤2kπ+$\frac{π}{3}$,k∈Z}.
点评 本题主要考查同角三角函数的基本关系的应用,三角不等式的解法,求函数的定义域,属于基础题.

练习册系列答案
相关题目
13.若关于x的不等式|x+3|-|x-1|>a2-3a的解集不空,则实数a的范围是( )
| A. | (-∞,-1)∪(4,+∞) | B. | (-1,4) | C. | (-∞,-4)∪(1,+∞) | D. | (-4,1) |
11.结合下面的算法:
第一步,输入x
第二步,判断x是否小于0,若是则输出x+2,结束程序;否则执行第三步
第三步,输出x-1,结束程序;
当输入的x的值分别是-1,0,1时,输出的结果分别为1,-1,0.
第一步,输入x
第二步,判断x是否小于0,若是则输出x+2,结束程序;否则执行第三步
第三步,输出x-1,结束程序;
当输入的x的值分别是-1,0,1时,输出的结果分别为1,-1,0.
13.用分析法证明问题时是从要证明的结论出发,逐步寻求使它成立的( )
| A. | 充要条件 | B. | 充分条件 | ||
| C. | 必要条件 | D. | 既不充分也不必要条件 |
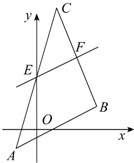 已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,且E、F分别是AC、BC的中点.求:
已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,且E、F分别是AC、BC的中点.求: