题目内容

20．已知函数f（x）=x2+4mx+n在区间[2，6]上是减函数，求实数m的取值范围（-∞，-3]．

分析 根据二次函数的对称轴与单调性的关系判断出[2，6]在对称轴左侧，列出不等式即可解出m的范围．

解答 解：f（x）=x2+4mx+n=（x+2m）2+n-4m2．
∴f（x）的图象开口向上，对称轴为x=-2m，
∴f（x）在（-∞，-2m]上单调递减，在[2m，+∞）上单调递增，
∵f（x）在区间[2，6]上是减函数，
∴6≤-2m，解的m≤-3．
故答案为（-∞，-3]．

点评 本题考查了二次函数的单调性，单调区间与对称轴的关系，属于中档题．

练习册系列答案
相关题目
10．有5名同学站成一排照相，则甲与乙相邻的不同排法种数有（　　）
A．8B．12C．36D．48
11．结合下面的算法：
第一步，输入x
第二步，判断x是否小于0，若是则输出x+2，结束程序；否则执行第三步
第三步，输出x-1，结束程序；
当输入的x的值分别是-1，0，1时，输出的结果分别为1，-1，0．
8．已知在直角坐标系xOy中，直线l的参数方程为是$\left\{\begin{array}{l}x=2+\frac{{\sqrt{2}}}{2}t\\ y=1+\frac{{\sqrt{2}}}{2}t\end{array}$（t为参数），以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ=4sinθ．
（1）判断直线l与曲线C的位置关系；
（2）在曲线C上求一点P，使得它到直线l的距离最大，并求出最大距离．
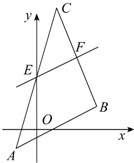15．已知△ABC的三顶点是A（-1，-1），B（3，1），C（1，6）．直线l平行于AB，交AC，BC分别于E，F，且E、F分别是AC、BC的中点．求：
（1）直线AB边上的高所在直线的方程．
（2）直线l所在直线的方程．
5．已知函数f（x）=2+log3x（1≤x≤9），函数g（x）=f2（x）+f（x2），求函数g（x）的值域．
12．已知条件p：（1-x）（x+1）＞0，条件q：-1＜x≤1，则￢p是￢q的必要不充分条件．
9．已知曲线C的参数方程为$\left\{\begin{array}{l}{x=2cosθ}\\{y=\sqrt{3}sinθ}\end{array}\right.$（θ为参数）．求曲线C的直角坐标方程，并指出曲线的类型．
10．已知椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）上的点到焦点的最大距离为3，离心率为$\frac{1}{2}$．
（1）求椭圆C的标准方程；
（2）设直线l：x-my+1=0与椭圆C交于不同两点A，B，与x轴交于点D，且满足$\overrightarrow{DA}$=λ$\overrightarrow{DB}$，若$-\frac{1}{2}$≤λ＜$-\frac{1}{3}$，求实数m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网