题目内容
在△ABC中，a，b，c分别是角A，B，C的对边，且b2=ac，sinB=
sinA．
（Ⅰ）求cosB．
（Ⅱ）若△ABC的面积为
，求BC边上中线的长．
| 2 |
（Ⅰ）求cosB．
（Ⅱ）若△ABC的面积为
| 7 |
考点：余弦定理,正弦定理
专题：三角函数的求值
分析：（Ⅰ）已知第二个等式利用正弦定理化简，将第一个等式代入表示出c，进而表示出b，利用余弦定理表示出cosB，将表示出的b与c代入即可求出cosB的值；
（Ⅱ）根据cosB的值，利用同角三角函数基本关系求出sinB的值，利用三角形面积公式表示出三角形ABC面积，将已知面积，c=2a以及sinB的值代入求出a的值，进而求出c的值，在三角形ABD中，利用余弦定理即可求出AD的长．
（Ⅱ）根据cosB的值，利用同角三角函数基本关系求出sinB的值，利用三角形面积公式表示出三角形ABC面积，将已知面积，c=2a以及sinB的值代入求出a的值，进而求出c的值，在三角形ABD中，利用余弦定理即可求出AD的长．
解答：
解：（Ⅰ）在△ABC中，由正弦定理化简sinB=
sinA，化简得：b=
a，
代入b2=ac，得：c=2a，
∴cosB=
=
=
；
（Ⅱ）由（Ⅰ）得：cosB=
，
∴sinB=
=
，
∵S△ABC=
acsinB=
•a•2a•
=
，
解得：a=2，
∴c=4，
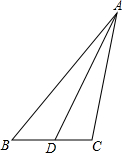
如图，取BC中点D，则BD=1，
在△ABD中，由余弦定理得：AD2=AB2+BD2-2AB•BDcosB=16+1-6=11，
则AD=
．
解：（Ⅰ）在△ABC中，由正弦定理化简sinB=| 2 |
| 2 |
代入b2=ac，得：c=2a，
∴cosB=
| a2+c2-b2 |
| 2ac |
| a2+4a2-2a2 |
| 4a2 |
| 3 |
| 4 |
（Ⅱ）由（Ⅰ）得：cosB=
| 3 |
| 4 |
∴sinB=
| 1-cos2B |
| ||
| 4 |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| 7 |
解得：a=2，
∴c=4，
如图，取BC中点D，则BD=1，
在△ABD中，由余弦定理得：AD2=AB2+BD2-2AB•BDcosB=16+1-6=11，
则AD=
| 11 |
点评：此题考查了正弦、余弦定理，以及三角形面积公式，熟练掌握定理及公式是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
| 2sin40°-cos10° |
| sin10° |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
已知椭圆C：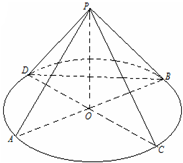
如图，AB，CD为圆O的两条直径，P为圆O所在平面外的一点，且PA=PB=PC
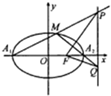如图，A1（-2，0），A2（2，0）是椭圆C：