题目内容
8．已知a、b为直线，a、β、γ为平面，下列两个命题（1）a⊥γ、b⊥γ、则a∥b
（2）a⊥b、a⊥α、则b∥α
其中有一个命题是正确的，正确的命题序号是（1）．
分析 利用空间直线与平面的平行与垂直判定及性质即可解决．
解答 解：对于（1），由垂直于同一平面的两直线平行，知结论正确；
对于（2），a⊥b、a⊥α、则b∥α或 b?α，故错
故答案为：（1）
点评 本题考查线面位置关系的判定及性质，属于基础题
练习册系列答案
相关题目
18．已知三棱锥P-ABC的四个顶点P，A，B，C都在半径为R的同一个球面上，若PA，PB，PC两两相互垂直，且PA=1，PB=2，PC=3，则R等于（ ）
| A． | $\frac{{\sqrt{14}}}{2}$ | B． | $\sqrt{14}$ | C． | $\frac{{\sqrt{13}}}{2}$ | D． | $\sqrt{3}$ |
16．
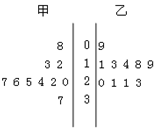某篮球队甲、乙两名运动员练习罚球，每人练习10组，每组罚球40个，命中个数的茎叶图如图所示，则下列结论错误 的一个是（ ）
某篮球队甲、乙两名运动员练习罚球，每人练习10组，每组罚球40个，命中个数的茎叶图如图所示，则下列结论错误 的一个是（ ）| A． | 甲的极差是29 | B． | 甲的中位数是25 | ||
| C． | 乙的众数是21 | D． | 甲的平均数比乙的大 |
3．已知$l_1^{\;}$∥α，$l_2^{\;}?α$，则直线$l_1^{\;}$与$l_2^{\;}$的位置关系是（ ）
| A． | 平行或异面 | B． | 异面 | C． | 相交 | D． | 以上都不对 |
20．甲、乙两个人投篮，他们投进篮的概率分别为$\frac{2}{5}，\frac{1}{2}$，现甲、乙两人各投篮1次，则两个人都投进的概率是（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{3}{10}$ | C． | $\frac{9}{10}$ | D． | $\frac{4}{5}$ |
17．下列命题中正确的是（ ）
| A． | 若p：?x∈R，ex＞xe，q：?x0∈R，|x0|≤0，则（￢p）∧q为假 | |
| B． | x=1是x2-x=0的必要不充分条件 | |
| C． | 直线ax+y+2=0与ax-y+4=0垂直的充要条件为a=±1 | |
| D． | “若xy=0，则x=0或y=0”的逆否命题为“若x≠0或y≠0，则xy≠0” |
