题目内容
13.设函数$f(x)=cos(2x+\frac{π}{3})+1$,如下结论中正确的是②③⑤.(写出所有正确结论的编号):①点$(-\frac{5}{12}π,0)$是函数f(x)图象的一个对称中心;
②直线x=$\frac{π}{3}$是函数f(x)图象的一条对称轴;
③函数f(x)的最小正周期是π;
④函数f(x)在$[-\frac{π}{6},\frac{π}{3}]$上为增函数;
⑤将函数f(x)的图象向右平移$\frac{π}{6}$个单位后,对应的函数是偶函数.
分析 ①,(-$\frac{5π}{12},1$)是函数f(x)图象的一个对称中心;
②,f($\frac{π}{3}$)=0为最小值,故直线x=$\frac{π}{3}$是函数f(x)图象的一条对称轴;
③,根据函数f(x)的正周期计算法则可得;
④,2×(-$\frac{π}{6}$)=-$\frac{π}{2}$,2×$\frac{π}{6}$=$\frac{π}{2}$,函数y=cosx在(-$\frac{π}{2},\frac{π}{2}$)上不单调;
⑤,将函数f(x)的图象向右平移$\frac{π}{6}$个单位后,对应的函数是y=cos2x+1,是偶函数;
解答 解:对于①,∵(-$\frac{5π}{12},1$)是函数f(x)图象的一个对称中心,故错;
对于②,∵f($\frac{π}{3}$)=0为最小值,故直线x=$\frac{π}{3}$是函数f(x)图象的一条对称轴,正确;
对于③,函数f(x)的最小正周期是π,正确;
对于④,2×(-$\frac{π}{6}$)=-$\frac{π}{2}$,2×$\frac{π}{6}$=$\frac{π}{2}$,函数y=cosx在(-$\frac{π}{2},\frac{π}{2}$)上不单调,故错;
对于⑤,将函数f(x)的图象向右平移$\frac{π}{6}$个单位后,对应的函数是y=cos2x+1,是偶函数,故正确;
故答案为:②③⑤
点评 本题考查了三角函数的图象及性质,属于基础题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
5.函数f(x)=ln|x-1|+2cosπx(-2≤x≤4)的所有零点之和等于( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
3.在复平面内,复数${({1-\sqrt{2}i})^2}$对应的点P位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
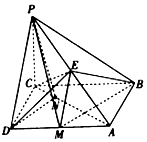 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是矩形,BC=PC,E是PA的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是矩形,BC=PC,E是PA的中点.