题目内容
17.已知函数f(x)=|x-2|+|2x+a|,a∈R.(Ⅰ)当a=1时,解不等式f(x)≥5;
(Ⅱ)若存在x0满足f(x0)+|x0-2|<3,求a的取值范围.
分析 (Ⅰ)当a=1时,根据绝对值不等式的解法即可解不等式f(x)≥5;
(Ⅱ)求出f(x)+|x-2|的最小值,根据不等式的关系转化为(f(x)+|x-2|)min<3即可求a的取值范围.
解答 解:(Ⅰ)当a=1时,f(x)=|x-2|+|2x+1|,.
由f(x)≥5得x-2|+|2x+1|≥5.
当x≥2时,不等式等价于x-2+2x+1≥5,解得x≥2,所以x≥2; …(1分)
当-$\frac{1}{2}$<x<2时,不等式等价于2-x+2x+1≥5,即x≥2,所以此时不等式无解;…(2分)
当x≤-$\frac{1}{2}$时,不等式等价于2-x-2x-1≥5,解得x≤-$\frac{4}{3}$,所以x≤-$\frac{4}{3}$.…(3分)
所以原不等式的解集为(-∞,-$\frac{4}{3}$]∪[2,+∞).…(5分)
(Ⅱ)f(x)+|x-2|=2|x-2|+|2x+a|=|2x-4|+|2x+a|≥|2x+a-(2x-4)|=|a+4|…(7分)
因为原命题等价于(f(x)+|x-2|)min<3,…(9分)
所以|a+4|<3,所以-7<a<-1为所求实数a的取值范围.…(10分)
点评 本题主要考查不等式的求解,根据绝对值不等式的解法,利用分类讨论的数学思想进行讨论是解决本题的关键.

练习册系列答案
相关题目
7.已知函数f(x)=$\frac{1}{3}$x3-(1+$\frac{b}{2}$)x2+2bx在区间(-3,1)上是减函数,则实数b的取值范围是( )
| A. | (-∞,-3] | B. | (-∞,1] | C. | [1,2] | D. | [-3,+∞) |
5.已知某大城市对每人车流量拥挤等级规定如表:
该城市对国庆节7天的车流量作出如表的统计数据:
(1)求该城市国庆节期间车流量的平均值与方差;
(2)某人国庆节连续2天到该城市游玩,求这2天他遇到的车流量拥挤等级均为严重拥挤的概率.
| 车流量(万辆) | 0~10 | 11~50 | 51~70 | 71~80 | 81~100 | >100 |
| 拥挤等级 | 优 | 良 | 轻度拥挤 | 中度拥挤 | 重度拥挤 | 严重拥挤 |
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 107日 |
| 车流量(万辆) | 120 | 110 | 85 | 75 | 60 | 105 | 110 |
(2)某人国庆节连续2天到该城市游玩,求这2天他遇到的车流量拥挤等级均为严重拥挤的概率.
12.已知函数f(x)=lnx-$\frac{1}{4}$x+$\frac{3}{4x}$-1,g(x)=x2-2bx+4,若对任意的x1∈(0,2)存在x2∈[1,2],使f(x1)≥g(x2),则实数b的取值范围是( )
| A. | [$\frac{17}{8}$,+∞) | B. | (-∞,$\frac{17}{8}$] | C. | (-∞,2] | D. | [2,+∞) |
9.2014年2月21日《中共中央关于全国深化改革若干重大问题的决定》明确:坚持计划生育的基本国策,启动实施一方是独生子女的夫妇可生育两个孩子的政策,为了解某地区城镇居民和农村居民对“单独两孩”的看法,某媒体在该地区选择了3600人调果,就是否赞成“单独两孩”的问题,调查统计的结果如下表:
已知在全体样本中随机抽取1人,抽到持“反对”态度的人的概率为0.05.
(1)现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“反对”态度的人中,用分层抽样的方法抽取6人,抽到农村居民和城镇居民各多少人?在抽取的6人中选取2人进行深入交流,求至少有1人为城镇居民的概率.
| 调查人群态度 | 赞成 | 反对 | 无所谓 |
| 农村居民 | 2100人 | 120人 | y人 |
| 城镇居民 | 600人 | x人 | z人 |
(1)现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“反对”态度的人中,用分层抽样的方法抽取6人,抽到农村居民和城镇居民各多少人?在抽取的6人中选取2人进行深入交流,求至少有1人为城镇居民的概率.
6.已知函数f(x)=$\left\{\begin{array}{l}{3^x},x≥0\\ 3x+1,x<0\end{array}\right.$,则不等式f(f(x))<4f(x)+1的解集是( )
| A. | (-3,0) | B. | (-$\frac{1}{3}$,1) | C. | (0,2) | D. | (-$\frac{1}{3}$,log32) |
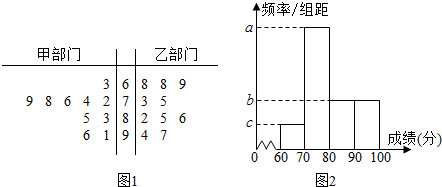
 长时间用手机上网严重影响着学生的身体健康,某校为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
长时间用手机上网严重影响着学生的身体健康,某校为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).