题目内容
已知O是△ABC内一点,且
+3
+3
=
,则△ABC的面积与△BOC的面积之比为 .
| OA |
| OB |
| OC |
| 0 |
考点:向量数乘的运算及其几何意义
专题:数形结合,平面向量及应用
分析:根据题意,求出
=
+
;再以OB、OC为邻边作平行四边形OBEC,得出
与
的关系,从而得出△ABC的面积与△BOC的面积的关系.
| 1 |
| 3 |
| AO |
| OB |
| OC |
| OE |
| AO |
解答:
解: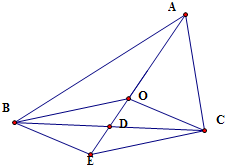 ∵
∵
+3
+3
=
,
∴
=-3
-3
=-3(
+
),
即
=
+
;
以OB、OC为邻边作平行四边形OBEC,
∴
=
+
=
,
∴点O在△ABC的中线AD上,且满足
=
;
∴OD=
AD,
∴△BOC的面积S△BOC=
S△ABC;
∴△ABC的面积与△BOC的面积之比为
=7.
故答案为:7.
 ∵
∵| OA |
| OB |
| OC |
| 0 |
∴
| OA |
| OB |
| OC |
| OB |
| OC |
即
| 1 |
| 3 |
| AO |
| OB |
| OC |
以OB、OC为邻边作平行四边形OBEC,
∴
| OE |
| OB |
| OC |
| 1 |
| 3 |
| AO |
∴点O在△ABC的中线AD上,且满足
| OD |
| 1 |
| 6 |
| AO |
∴OD=
| 1 |
| 7 |
∴△BOC的面积S△BOC=
| 1 |
| 7 |
∴△ABC的面积与△BOC的面积之比为
| S△ABC |
| S△BOC |
故答案为:7.
点评:本题考查了平面向量加法的几何意义的应用问题,也考查了数形结合的应用问题,是基础题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)单调递增,若实数a满足f(log2a)+f(log
a)≤2f(1),则a的取值范围是( )
| 1 |
| 2 |
A、[
| ||
B、[
| ||
C、[
| ||
| D、(0,2] |
设向量
=(m-2,m+3),
=(2m+1,m-2),若
与
的夹角大于90°,则实数m的取值范围是( )
| a |
| b |
| a |
| b |
A、(-
| ||
B、(-∞,-
| ||
C、(-2,
| ||
D、(-∞,2)∪(
|