题目内容

1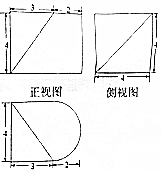．某几何体的三视图如图所示（其中俯视图中的圆弧是半圆），则该几何体的体积为32+8π．

分析 根据几何体的三视图，得出该几何体是多面体与半圆柱体的组合体，画出图形结合图形求出它的体积．

解答 解：根据几何体的三视图，得；
该几何体是长方体与半圆柱体的组合体，且在长方体的顶点处截去一个四棱锥，
如图所示；
所以该组合体的体积为
V几何体=V多面体+V半圆柱体
=（3×4×4-$\frac{1}{3}$×4×4×3）+$\frac{1}{2}$π×22×4
=32+8π．
故答案为：32+8π．

点评 本题考查了空间几何体三视图的应用问题，解题的关键是根据三视图画出几何体，是基础题．

练习册系列答案
相关题目
11．如图，一张A4纸的长、宽分别为2$\sqrt{2}$a，2a，A，B，C，D分别是其四条边的中点，现将其沿图中虚线折起，使得P1，P2，P3，P4四点重合为一点P，从而得到一个多面体，关于该多面体的下列命题，正确的是①②③④．（写出所有正确命题的序号）．
①该多面体是三棱锥；②平面BAD⊥平面BCD；
③平面BAC⊥平面ACD；④该多面体外接球的表面积为5πa2．
12．求以原点为顶点，坐标轴为对称轴，并且经过点P（-4，-2）的抛物线的标准方程．
9．已知椭圆Γ的左、右焦点分别为F1（-1，0）、F2（1，0）．经过点F1且倾斜角为θ（0＜θ＜π）的直线l与椭圆Γ交于A、B两点（其中点A在x轴上方），△ABF2的周长为8．
（1）求椭圆Γ的标准方程；
（2）如图，把平面xOy沿x轴折起来，使y轴正半轴和x轴确定的半平面，与y负半轴和x轴所确定的半平面互相垂直．
①若θ=$\frac{π}{3}$，求异面直线AF1和BF2所成角的大小；
②若折叠后△ABF2的周长为$\frac{15}{2}$，求θ的大小．
16．已知函数f（x）=（2x2-x-1）ex，则方程${[{ef（x）}]^2}+tf（x）-9\sqrt{e}=0$（t∈R）的根的个数为（　　）
A．3B．2C．5D．4
6．如图为某几何体的三视图，则该几何体的外接球的直径为（　　）
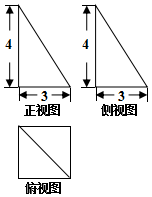
A．10B．$\sqrt{34}$C．5D．$\frac{{\sqrt{34}}}{2}$
13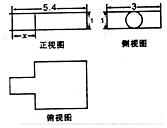．中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器-商鞅铜方升，其三视图如图所示（单位：寸），若π取3，其体积为13.5（立方寸），则图中的x为（　　）
A．2.4B．1.8C．1.6D．1.2
10．在直角坐标系xOy中，曲线C1的参数方程为$\left\{\begin{array}{l}{x=-3+t}\\{y=-1-t}\end{array}\right.$（t为参数），以坐标原点O为极点，以x轴正半轴为极轴，建立极坐标系，圆C2的极坐标方程为ρ=4$\sqrt{2}$sin（$\frac{3π}{4}$-θ）．
（Ⅰ）求C1的普通方程和C2的直角坐标方程；
（Ⅱ）设点M为曲线C1上任意一点，过M作圆C2的切线，切点为N，求|MN|的最小值．
11．已知两条直线m，n和两个不同平面α，β，满足α⊥β，α∩β=l，m∥α，n⊥β，则（　　）
A．m∥nB．m⊥nC．m∥lD．n⊥l

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网