题目内容
三双不同品牌的鞋排成一排,则相邻的鞋都为不同品牌的概率是 .
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:根据6只鞋全排列:|s|=6!,Ai表示第i双相邻的排列|Ai|=2•5!,|Ai•Aj|=22•4!,|Ai•AJ•Ak|=23•3!,求出|
•
•
|=10×4!,进而求解.
. |
| A1 |
. |
| A2 |
. |
| A3 |
解答:
解:6只鞋全排列:|s|=6!,
Ai表示第i双相邻的排列|Ai|=2•5!,
|Ai•Aj|=22•4!,|Ai•AJ•Ak|=23•3!,
|
•
•
|=6!-(
•2•5!-
•22•4!
•23•3!)=10×4!,
所以相邻的鞋都为不同品牌的概率P(0)=
=
.
故答案为:
.
Ai表示第i双相邻的排列|Ai|=2•5!,
|Ai•Aj|=22•4!,|Ai•AJ•Ak|=23•3!,
|
. |
| A1 |
. |
| A2 |
. |
| A3 |
| C | 1 3 |
| C | 2 3 |
| +C | 3 3 |
所以相邻的鞋都为不同品牌的概率P(0)=
| 4!×10 |
| 6! |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题主要考察了概率的相关解法,属于基础题.

练习册系列答案
相关题目
已知数列{an}中,a1=2,an+1=an+
(n∈N+),则a101=( )
| 1 |
| 2 |
| A、50 | B、51 | C、52 | D、53 |
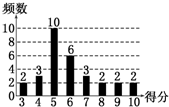 为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为me,众数为m0,平均值为
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为me,众数为m0,平均值为. |
| x |
A、me=m0=
| ||
B、me=m0<
| ||
C、me<m0<
| ||
D、m0<me<
|
已知f(x)是一次函数,若f(0)=1,f(2x)=f(x)+x,则f(x)=( )
| A、2x+1 | B、x+1 |
| C、x | D、2x |
 如图,正方体中ABCD-A1B1C1D1中,E、F分别为BB1、D1B1中点.
如图,正方体中ABCD-A1B1C1D1中,E、F分别为BB1、D1B1中点.