Question

设点（a，b）是区域

2x+y-4≤0 x＞0 y＞0

内的随机点，函数f（x）=ax²-4bx+1在区间[1，+∞）上是增函数的概率为（　　）

• A、

  1

  2

• B、

  1

  3

• C、

  1

  4

• D、

  1

  5

Answer 1

考点：几何概型,二元一次不等式（组）与平面区域

专题：概率与统计

分析：作出不等式组对应的平面区域，求出f（x）=ax²-4bx+1在区间[1，+∞）上是增函数的等价条件，利用几何概型的概率公式即可得到结论．

解答： 解：作出不等式组对应的平面区域如图为三角形OBC：面积为

1

2

×2×4=4，
则a＞0．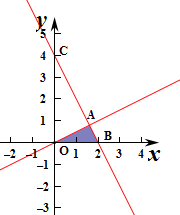
若f（x）=ax²-4bx+1在区间[1，+∞）上是增函数，
则对称轴x=-

-4b

2a

=

2b

a

≤1，即a≥2b，对应的平面区域如图（阴影部分三角形OAB），
由

2x+y-4=0 x=2y

，解得

x= 8 5 y= 4 5

，即A（

8

5

，

4

5

），
则三角形OAB的面积S

1

2

×2×

4

5

=

4

5

，
则函数f（x）=ax²-4bx+1在区间[1，+∞）上是增函数的概率

4 5

4

=

1

5

，
故选：D

点评：本题主要考查几何概型的概率的计算，根据不等式组做出对应的平面区域，求出对应的面积是解决本题的关键．