题目内容
14.已知数列{an}满足a1=3,an+1an+an+1-an+1=0,n∈N*,则a2016=( )| A. | -2 | B. | $-\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 3 |
分析 数列{an}满足a1=3,an+1an+an+1-an+1=0,n∈N*,可得:an+4=an.即可得出.
解答 解:∵数列{an}满足a1=3,an+1an+an+1-an+1=0,n∈N*,
∴an+1=$\frac{{a}_{n}-1}{{a}_{n}+1}$,a2=$\frac{3-1}{3+1}$=$\frac{1}{2}$,同理可得:a3=-$\frac{1}{3}$.a4=-2,a5=3,…,
an+4=an.
∴a2016=a503×4+4=a4=-2.
故选:A.
点评 本题考查了数列递推关系、周期性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.如图,给出抛物线和其对称轴上的四个点P、Q、R、S,则抛物线的焦点是( )


| A. | P | B. | Q | C. | R | D. | S |
9.设a,b∈R,i是虚数单位,则“$a=\sqrt{3}$,b=1”是“$|{\frac{1+bi}{a+i}}|=\frac{{\sqrt{2}}}{2}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.凸十边形的对角线的条数为( )
| A. | 10 | B. | 35 | C. | 45 | D. | 90 |
14.如图所示的程序框图,若输入m=8,n=3,则输出的S值为( )
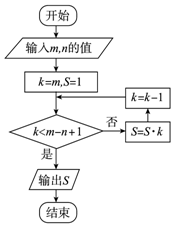

| A. | 56 | B. | 336 | C. | 360 | D. | 1440 |