题目内容
14.如图所示的程序框图,若输入m=8,n=3,则输出的S值为( )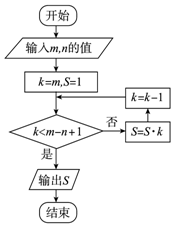
| A. | 56 | B. | 336 | C. | 360 | D. | 1440 |
分析 执行程序框图,依次写出每次循环得到的s,k的值,k=5时,满足条件k<m-n+1,退出循环,输出s的值为336.
解答 解:执行程序框图,可得
m=8,n=3,
k=8,s=1
不满足条件k<m-n+1,s=8,k=7,
不满足条件k<m-n+1,s=56,k=6,
不满足条件k<m-n+1,s=336,k=5,
满足条件k<m-n+1,退出循环,输出s的值为336.
故选:B.
点评 本题主要考察了程序框图和算法,正确得到每次循环s的值是解题的关键,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
14.已知数列{an}满足a1=3,an+1an+an+1-an+1=0,n∈N*,则a2016=( )
| A. | -2 | B. | $-\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 3 |
19.如表提供了工厂技术改造后某种型号设备的使用年限x和所支出的维修费用y(万元)的几组对照数据:
(1)若知道y对x呈线性相关关系,请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=bx+a
(2)已知工厂技改前该型号设备使用10年的维修费用为9万元.试根据(1)求出的线性回归方程,预测该型号设备技改后使用10年的维修费用比技改前降低多少?
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=y-$\stackrel{∧}{b}$x.
| x(年) | 3 | 4 | 5 | 6 |
| y(万元) | 2.5 | 3 | 4 | 4.5 |
(2)已知工厂技改前该型号设备使用10年的维修费用为9万元.试根据(1)求出的线性回归方程,预测该型号设备技改后使用10年的维修费用比技改前降低多少?
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=y-$\stackrel{∧}{b}$x.
6.已知复数z满足(3+4i)z=25,则z对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
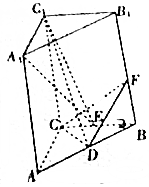 如图,三棱柱ABC-A1B1C1中,CC1⊥平面ABC,∠ACB=90°,BB1=3,AC=BC=2,D,E分别为AB,BC的中点,F为BB1上一点,且$\frac{BF}{F{B}_{1}}$=$\frac{2}{7}$.
如图,三棱柱ABC-A1B1C1中,CC1⊥平面ABC,∠ACB=90°,BB1=3,AC=BC=2,D,E分别为AB,BC的中点,F为BB1上一点,且$\frac{BF}{F{B}_{1}}$=$\frac{2}{7}$.