题目内容
18.对满足条件x≥0,y≥0,x+y≤2的实数x,y,记z=|x-1|+|y-1|,则z的最大值为( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
分析 作出不等式组对应的平面区域,根据绝对值的意义,利用分类讨论的数学,进行平移即可.
解答 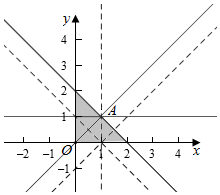 解:由z=|x-1|+|y-1|,得|y-1|=-|x-1|+z,
解:由z=|x-1|+|y-1|,得|y-1|=-|x-1|+z,
当y≥1时,y-1=-|x-1|+z,即y=-|x-1|+z+1,
当y<1时,-(y-1)=-|x-1|+z,即y=|x-1|+1-z,
作出不等式组对应的平面区域如图:
当y≥1时,平移曲线y=-|x-1|+z+1,由图象知当直线经过A时,曲线对应的z最大,
由$\left\{\begin{array}{l}{y=1}\\{x+y=2}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,即A(1,1),此时z=|x-1|+|y-1|=0,
当y<1时平移曲线y=|x-1|+1-z,由图象知当直线经过(1,0)时,曲线对应的z最大,
此时z=|x-1|+|y-1|=0+1=1,
综上,z的最大值为1,
故选:A
点评 本题主要考查线性规划的应用,利用数形结合以及分类讨论的数学是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
相关题目
6.$\frac{tan\frac{π}{8}}{1-ta{n}^{2}\frac{π}{8}}$等于( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
13.已知函数f(x)=-sin$\frac{π}{2}$x-1,g(x)=logax(a>0且a≠1),若F(x)=f(x)-g(x)至少有三个零点,则实数a的取值范围是( )
| A. | (0,$\frac{\sqrt{5}}{5}$) | B. | ($\frac{\sqrt{5}}{5}$,1) | C. | ($\frac{\sqrt{3}}{3}$,1) | D. | (0,$\frac{\sqrt{3}}{3}$) |
17.已知A,B分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右顶点,P是双曲线C右支上位于第一象限的动点,设PA,PB的斜率分别为k1,k2,则k1+k2的取值范围为( )
| A. | ($\frac{2b}{a}$,+∞) | B. | ($\frac{b}{a}$,+∞) | C. | [$\frac{b}{a}$,+∞) | D. | [$\frac{b}{a}$,$\frac{2b}{a}$) |
18.数列{an}满足a1=1,且an+1=a1+an+n(n∈N*),则$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2016}}$等于( )
| A. | $\frac{2015}{2016}$ | B. | $\frac{4028}{2015}$ | C. | $\frac{4032}{2017}$ | D. | $\frac{2014}{2015}$ |
