题目内容
已知y=f（x）为R上的可导函数，当x≠0时，f′（x）+
＞0，则关于的函数g（x）=f（x）+
的零点个数为（ ）
| f(x) |
| x |
| 2 |
| x |
| A、0 | B、1 |
| C、2 | D、0或 2 |
考点：根的存在性及根的个数判断,函数零点的判定定理
专题：计算题,函数的性质及应用
分析：由题意，g（x）的零点与xg（x）的非零零点是完全一样的，讨论xg（x）的非零零点即可．
解答：
解：∵g（x）=f（x）+
，∴x≠0；
∴g（x）的零点与xg（x）的非零零点是完全一样的，
∵（xg（x））'=（xf（x））'=xf'（x）+f（x）
=x（ f'（x）+
），
又∵f′（x）+
＞0，
∴（0，+∞）上，xg（x）单调递增，
∵f（x） R上可导，∴f（x）在0处连续，
∴
（ xf（x）+2）=2，
∴在（0，+∞）上没有g（x）的零点；
同理，在（-∞，0）上也没有g（x）的零点；
∴函数g（x）=f（x）+
的零点个数为0．
故选A．
| 2 |
| x |
∴g（x）的零点与xg（x）的非零零点是完全一样的，
∵（xg（x））'=（xf（x））'=xf'（x）+f（x）
=x（ f'（x）+
| f(x) |
| x |
又∵f′（x）+
| f(x) |
| x |
∴（0，+∞）上，xg（x）单调递增，
∵f（x） R上可导，∴f（x）在0处连续，
∴
| lim |
| x→0 |
∴在（0，+∞）上没有g（x）的零点；
同理，在（-∞，0）上也没有g（x）的零点；
∴函数g（x）=f（x）+
| 2 |
| x |
故选A．
点评：本题考查了根的存在性定理及函数的单调性的应用，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
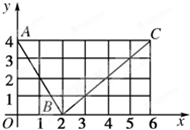如图所示折线段ABC，其中A、B、C的坐标分别为（0，4），（2，0），（6，4）．