题目内容
12.已知f(x)是定义在R上的偶函数,当x≥0时,f(x)=$\left\{\begin{array}{l}{|{x}^{2}-1|,0≤x≤2}\\{f(x-1),x>2}\\{\;}\end{array}\right.$,若方程f(x)=kx恰有4个不同的根,则实数k的取值范围是$\frac{3}{5}$<k≤$\frac{3}{4}$或-$\frac{3}{4}$≤k<-$\frac{3}{5}$.分析 根据条件作出函数f(x)的图象,利用数形结合建立g(x)=kx与f(x)的大小关系即可得到结论.
解答 解:当2<x≤3时,1<x-1≤2,
则f(x)=f(x-1)=|(x-1)2-1|,
∵函数f(x)是偶函数,作出函数f(x)的图象如图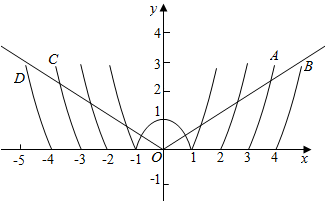
∴若方程f(x)=kx恰有4个不同的根,
则等价为函数g(x)=kx在AB之间或在CD之间(包含C,A),
f(5)=f(4)=f(3)=f(2)=3,
要使f(x)=kx恰有4个不同的根,则满足$\left\{\begin{array}{l}{g(4)=4k≤3}\\{g(5)=5k>3}\end{array}\right.$或$\left\{\begin{array}{l}{g(-4)=-4k≤3}\\{g(-5k)=-5k>3}\end{array}\right.$,
即$\left\{\begin{array}{l}{k≤\frac{3}{4}}\\{k>\frac{3}{5}}\end{array}\right.$或$\left\{\begin{array}{l}{k≥-\frac{3}{4}}\\{k<-\frac{3}{5}}\end{array}\right.$,
即$\frac{3}{5}$<k≤$\frac{3}{4}$或-$\frac{3}{4}$≤k<-$\frac{3}{5}$,
故答案为:$\frac{3}{5}$<k≤$\frac{3}{4}$或-$\frac{3}{4}$≤k<-$\frac{3}{5}$,
点评 本题主要考查函数与方程的应用,作出函数的图象,利用数形结合是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.平面直角坐标系xOy中,双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线与抛物线C2:y2=2px(p>0)交于点O,A,B,若△OAB的重心为C2的焦点,则C1的渐近线方程为( )
| A. | y=±$\frac{\sqrt{6}}{4}$x | B. | y=±$\frac{2\sqrt{6}}{3}$x | C. | y=±2$\sqrt{2}$x | D. | y=±$\frac{2\sqrt{3}}{3}$x |
20.已知点F1、F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,O为坐标原点,点P在双曲线C的右支上,且满足|F1F2|=2|OP|,|PF1|≥3|PF2|,则双曲线C的离心率的取值范围为( )
| A. | (1,+∞) | B. | [$\frac{\sqrt{10}}{2}$,+∞) | C. | (1,$\frac{\sqrt{10}}{2}$] | D. | (1,$\frac{5}{2}$] |
 某几何体的三视图如图所示,正视图与侧视图完全相同,则该几何体的体积为$\frac{64-8π}{3}$.
某几何体的三视图如图所示,正视图与侧视图完全相同,则该几何体的体积为$\frac{64-8π}{3}$.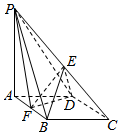 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=3,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=3,PA⊥平面ABCD,E是PC的中点,F是AB的中点. 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),圆Q:(x-2)2+(y-$\sqrt{2}$)2=2的圆心Q在椭圆C上,点P(0,$\sqrt{2}$)到椭圆C的右焦点的距离为$\sqrt{6}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),圆Q:(x-2)2+(y-$\sqrt{2}$)2=2的圆心Q在椭圆C上,点P(0,$\sqrt{2}$)到椭圆C的右焦点的距离为$\sqrt{6}$.