题目内容
12.命题p:?x∈N,x3<x2;命题q:?a∈(0,1),函数f(x)=logax在其定义域内单调递减,则真命题是( )| A. | ¬q | B. | p∧q | C. | ¬p∧q | D. | p∧(¬q) |
分析 命题p:如图所示,利用几何画板即可判断出真假.命题q:利用对数函数的单调性即可判断出真假.
解答  解:命题p:如图所示,可知:函数y=x3与y=x2有且只有两个交点,(0,0),(1,1),因此:不存在x∈N,x3<x2,命题p是假命题.
解:命题p:如图所示,可知:函数y=x3与y=x2有且只有两个交点,(0,0),(1,1),因此:不存在x∈N,x3<x2,命题p是假命题.
命题q:?a∈(0,1),函数f(x)=logax在其定义域内单调递减,是真命题.
只有¬p∧q是真命题.
故选:C.
点评 本题考查了函数的单调性、复合命题真假的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
3.定义在R上的函数f(x)满足:f(x+4)=f(x),f(x)=$\left\{\begin{array}{l}{2x,x∈(-1.1]}\\{-{x}^{2}+2x+1,x∈(1,3]}\\{\;}\end{array}\right.$,当x∈[0,+∞)时,方程f(x)-4xa=0(a>0)有且只有3个不等实根,则实数a的值为(e是自然对数底数)( )
| A. | $\frac{1}{{2}^{8}eln2}$ | B. | $\frac{1}{{2}^{9}}$ | C. | $\frac{e}{{2}^{8}ln2}$ | D. | $\frac{e}{{2}^{9}}$ |
20.正态分布ξ~N(a,32),且P(ξ<2a-3)=P(ξ>a+2),则a的值为( )
| A. | $\frac{7}{3}$ | B. | $\frac{4}{3}$ | C. | 1 | D. | 4 |
17.已知k∈Z,$\overrightarrow{AB}$=(k,1),$\overrightarrow{BC}$=(k-2,-3),若|$\overrightarrow{AB}$|≤$\sqrt{17}$,则∠ABC是直角的概率是( )
| A. | $\frac{4}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{9}$ |
20.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F作一条直线,当直线倾斜角为$\frac{π}{6}$时,直线与双曲线左、右两支各有一个交点;当直线倾斜角为$\frac{π}{3}$时,直线与双曲线右支有两个不同的交点,则双曲线离心率的取值范围为( )
| A. | $({1,\frac{{2\sqrt{3}}}{3}})$ | B. | $({\frac{{2\sqrt{3}}}{3},2})$ | C. | $(1,\sqrt{3})$ | D. | (1,2) |
 如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,AM=2.
如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,AM=2.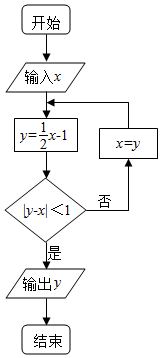
 某几何体的三视图如图所示,正视图与侧视图完全相同,则该几何体的体积为$\frac{64-8π}{3}$.
某几何体的三视图如图所示,正视图与侧视图完全相同,则该几何体的体积为$\frac{64-8π}{3}$.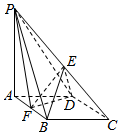 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=3,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=3,PA⊥平面ABCD,E是PC的中点,F是AB的中点.