题目内容
12.执行如图所示的程序框图,若依次输入m=${0.6^{\frac{1}{2}}}$,n=0.6-2,p=${({\frac{1}{3}})^{\frac{1}{2}}}$,则输出的结果为( )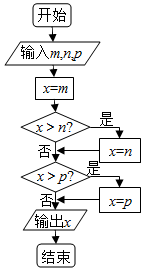
| A. | ${({\frac{1}{3}})^{\frac{1}{2}}}$ | B. | ${0.6^{\frac{1}{2}}}$ | C. | 0.6-2 | D. | ${0.6^{-\frac{3}{2}}}$ |
分析 模拟执行程序,可得该流程图的作用是求出m、n、p中的最小数,化简比较三个数即可得解.
解答 解:根据题意,该流程图的作用是求出m、n、p中的最小数,
并将此最小的数用变量x表示并输出,
由于,m=${0.6^{\frac{1}{2}}}$=$\frac{\sqrt{15}}{5}$,n=0.6-2=$\frac{25}{9}$,p=${({\frac{1}{3}})^{\frac{1}{2}}}$=$\frac{\sqrt{3}}{3}$,
可得,$\frac{25}{9}$>$\frac{\sqrt{15}}{5}$>$\frac{\sqrt{3}}{3}$,即:n>m>p.
故选:A.
点评 本题主要考查了选择结构的程序框图,属于基础题.解题的关键是先根据已知条件判断程序的功能,读懂各部分的作用再求解,从而使问题得以解决.

练习册系列答案
相关题目
20.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F作一条直线,当直线倾斜角为$\frac{π}{6}$时,直线与双曲线左、右两支各有一个交点;当直线倾斜角为$\frac{π}{3}$时,直线与双曲线右支有两个不同的交点,则双曲线离心率的取值范围为( )
| A. | $({1,\frac{{2\sqrt{3}}}{3}})$ | B. | $({\frac{{2\sqrt{3}}}{3},2})$ | C. | $(1,\sqrt{3})$ | D. | (1,2) |
17.某高校一专业在一次自主招生中,对20名已经选拔入围的学生进行语言表达能力和逻辑思维能力测试,结果如表:
由于部分数据丢失,只知道从这20名参加测试的学生中随机抽取一人,抽到语言表达能力优秀或逻辑思维能力优秀的学生的概率为$\frac{2}{5}$.
(1)求m,n的值;
(2)从参加测试的语言表达能力良好的学生中任意抽取2名,求其中至少有一名逻辑思维能力优秀的学生的概率.
| 语言表达能力 人数 逻辑思维能力 | 一般 | 良好 | 优秀 |
| 一般 | 2 | 2 | 1 |
| 良好 | 4 | m | 1 |
| 优秀 | 1 | 3 | n |
(1)求m,n的值;
(2)从参加测试的语言表达能力良好的学生中任意抽取2名,求其中至少有一名逻辑思维能力优秀的学生的概率.
20.已知点F1、F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,O为坐标原点,点P在双曲线C的右支上,且满足|F1F2|=2|OP|,|PF1|≥3|PF2|,则双曲线C的离心率的取值范围为( )
| A. | (1,+∞) | B. | [$\frac{\sqrt{10}}{2}$,+∞) | C. | (1,$\frac{\sqrt{10}}{2}$] | D. | (1,$\frac{5}{2}$] |
 如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,AM=2.
如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,AM=2. 某几何体的三视图如图所示,正视图与侧视图完全相同,则该几何体的体积为$\frac{64-8π}{3}$.
某几何体的三视图如图所示,正视图与侧视图完全相同,则该几何体的体积为$\frac{64-8π}{3}$.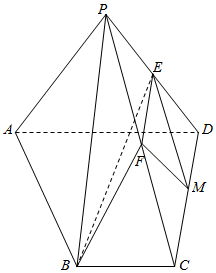 如图所示,已知在四棱锥P-ABCD中,底面四边形ABCD是直角梯形,BC∥AD,BC⊥CD,AD=CD=2BC=4,△PAD是等边三角形,平面PAD⊥平面ABCD,E,F分别是PD,PC的中点,M为CD上一点.
如图所示,已知在四棱锥P-ABCD中,底面四边形ABCD是直角梯形,BC∥AD,BC⊥CD,AD=CD=2BC=4,△PAD是等边三角形,平面PAD⊥平面ABCD,E,F分别是PD,PC的中点,M为CD上一点.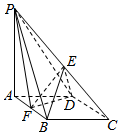 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=3,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=3,PA⊥平面ABCD,E是PC的中点,F是AB的中点.