题目内容
已知点F(1,0),直线l:x=-1,动点P到点F的距离与到直线l的距离相等.
(Ⅰ)求动点P的轨迹C的方程;
(Ⅱ)直线y=
x+b与曲线C交于A,B两点,若曲线C上存在点D使得四边形FABD为平行四边形,求b的值.
(Ⅰ)求动点P的轨迹C的方程;
(Ⅱ)直线y=
| 3 |
考点:轨迹方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据抛物线的定义,可求动点P的轨迹C的方程;
(Ⅱ)解法一:直线与抛物线联立,解得D点的横坐标,计算出|FD|,|AB|,利用FABD为平行四边形,所以|AB|=|FD|,建立方程,即可求b的值;解法二:先求出D的坐标,再分类讨论,利用韦达定理,结合四边形是平行四边形,所以
+
=
,即可求b的值.
(Ⅱ)解法一:直线与抛物线联立,解得D点的横坐标,计算出|FD|,|AB|,利用FABD为平行四边形,所以|AB|=|FD|,建立方程,即可求b的值;解法二:先求出D的坐标,再分类讨论,利用韦达定理,结合四边形是平行四边形,所以
| FA |
| FD |
| FB |
解答:
解:(Ⅰ)依题意,动点P的轨迹C是以F(1,0)为焦点,l:x=-1为准线的抛物线,
设轨迹C的方程为y2=2px(p>0),则p=2所以动点P的轨迹C的方程为 y2=4x,
(Ⅱ)解法一:因为F(1,0),故直线FD的方程为y=
(x-1),
联立方程组
消元得:3x2-10x+3=0,解得D点的横坐标为x=3或x=
.
由抛物线定义知:|FD|=x+
=4或
,
又由
消元得:
y2-4y+4b=0.
设A(x1,y1),B(x2,y2),
则△=16-16
b>0且
所以|AB|=
•|y1-y2|=
•
,
因为FABD为平行四边形,所以|AB|=|FD|,
所以
•
=4或
,
解得b=-
或
,代入△>0成立.
解法二:因为F(1,0),故直线FD的方程为y=
(x-1),
联立方程组
消元得:3x2-10x+3=0,解得x=3或x=
,
故点D(3,2
)或D(
,-
),
当D(3,2
)时,设A(x1,y1),B(x2,y2),
联立方程组
消元得:3x2+(2
b-4)x+b2=0(*)
根据韦达定理有x1+x2=-
①,x1•x2=
②,
又因为四边形是平行四边形,所以
+
=
,将坐标代入有x2=x1+2③,
代入①有x1=
,x2=
,
代入②有
•
=
,整理得b=-
此时(*)的判别式△>0,符合题意
当D(
,-
)时,同理可解得b=
.
设轨迹C的方程为y2=2px(p>0),则p=2所以动点P的轨迹C的方程为 y2=4x,
(Ⅱ)解法一:因为F(1,0),故直线FD的方程为y=
| 3 |
联立方程组
|
消元得:3x2-10x+3=0,解得D点的横坐标为x=3或x=
| 1 |
| 3 |
由抛物线定义知:|FD|=x+
| p |
| 2 |
| 4 |
| 3 |
又由
|
| 3 |
设A(x1,y1),B(x2,y2),
则△=16-16
| 3 |
|
所以|AB|=
| 1+3 |
| 8 |
| 3 |
1-
|
因为FABD为平行四边形,所以|AB|=|FD|,
所以
| 8 |
| 3 |
1-
|
| 4 |
| 3 |
解得b=-
5
| ||
| 12 |
| ||
| 4 |
解法二:因为F(1,0),故直线FD的方程为y=
| 3 |
联立方程组
|
| 1 |
| 3 |
故点D(3,2
| 3 |
| 1 |
| 3 |
2
| ||
| 3 |
当D(3,2
| 3 |
联立方程组
|
| 3 |
根据韦达定理有x1+x2=-
2
| ||
| 3 |
| b2 |
| 3 |
又因为四边形是平行四边形,所以
| FA |
| FD |
| FB |
代入①有x1=
-
| ||
| 3 |
-
| ||
| 3 |
代入②有
-
| ||
| 3 |
-
| ||
| 3 |
| b2 |
| 3 |
5
| ||
| 12 |
此时(*)的判别式△>0,符合题意
当D(
| 1 |
| 3 |
2
| ||
| 3 |
| ||
| 4 |
点评:定义法是求圆锥曲线方程的重要方法,解决直线与圆锥曲线位置关系问题,通常联立方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知sin(θ-
)=2cos(θ+
),则
=( )
| π |
| 4 |
| π |
| 4 |
sin(
| ||
sin(
|
| A、-4 | ||
| B、-2 | ||
C、
| ||
| D、-1 |
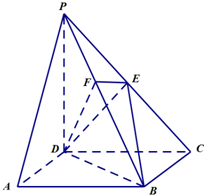 如图,在四棱锥P-ABCD中,侧面PDC⊥底面ABCD,已知△PDC是等腰直角三角形,其中∠PDC为直角,底面ABCD是边长为2的正方形,E是PC的中点,F是PB上的点.
如图,在四棱锥P-ABCD中,侧面PDC⊥底面ABCD,已知△PDC是等腰直角三角形,其中∠PDC为直角,底面ABCD是边长为2的正方形,E是PC的中点,F是PB上的点.