题目内容
已知中心在原点,焦点在x轴上的椭圆焦距为2,离心率为
(1)求椭圆的标准方程
(2)若直线l过点(1,2)且倾斜角为45°且与椭圆相交于A,B两点,求弦长|AB|.
| 1 |
| 2 |
(1)求椭圆的标准方程
(2)若直线l过点(1,2)且倾斜角为45°且与椭圆相交于A,B两点,求弦长|AB|.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)根据焦点在x轴上的椭圆焦距为2,离心率为
,可得c=1,
=
,求出几何量,可得椭圆的标准方程;
(2)直线l的方程为y=x+1,代入椭圆方程,消去y可得7x2+8x-8=0,利用弦长公式可得结论.
| 1 |
| 2 |
| c |
| a |
| 1 |
| 2 |
(2)直线l的方程为y=x+1,代入椭圆方程,消去y可得7x2+8x-8=0,利用弦长公式可得结论.
解答:
解:(1)∵焦点在x轴上的椭圆焦距为2,离心率为
,
∴c=1,
=
,
∴a=2,
∴b2=a2-c2=3,
∴所求椭圆方程为
+
=1;
(2)设A(x1,y1),B(x2,y2),则
∵直线l过点(1,2)且倾斜角为45°,
∴直线l的方程为y=x+1,
代入椭圆方程,消去y可得7x2+8x-8=0,
∴x1+x2=-
,x1x2=-
∴|x1-x2|=
=
因此,|AB|=
•|x1-x2|=
.
| 1 |
| 2 |
∴c=1,
| c |
| a |
| 1 |
| 2 |
∴a=2,
∴b2=a2-c2=3,
∴所求椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)设A(x1,y1),B(x2,y2),则
∵直线l过点(1,2)且倾斜角为45°,
∴直线l的方程为y=x+1,
代入椭圆方程,消去y可得7x2+8x-8=0,
∴x1+x2=-
| 8 |
| 7 |
| 8 |
| 7 |
∴|x1-x2|=
(
|
12
| ||
| 7 |
因此,|AB|=
| 2 |
| 24 |
| 7 |
点评:本题考查椭圆的标准方程与几何性质,考查直线与椭圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
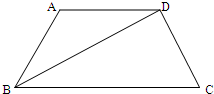 如图,在四边形ABCD中,
如图,在四边形ABCD中,