题目内容
已知函数y=ax2+bx+c的图象过(0,-1)、(2,5)、(-3,20)三点.
(1)求这个函数的解析式;
(2)求函数的顶点坐标和对称轴;
(3)求函数的单调区间及最值.
(1)求这个函数的解析式;
(2)求函数的顶点坐标和对称轴;
(3)求函数的单调区间及最值.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)利用待定系数法求解析式;
(2)对解析式配方,确定顶点坐标和对称轴;
(3)由(2)确定函数的单调区间及最值.
(2)对解析式配方,确定顶点坐标和对称轴;
(3)由(2)确定函数的单调区间及最值.
解答:
解:(1)由题意,设二次函数解析式为y=ax2+bx+c,因为图象过(0,-1)、(2,5)、(-3,20)三点.
所以
解得
,
所以这个函数的解析式y=2x2-x-1;
(2)由(1)得y=2(x-
)2-
,所以函数的顶点坐标为(
,-
),对称轴为x=
;
(3)由(2)得y=2(x-
)2-
,所以函数的单调增区间为[
,+∞),单调减区间为(-∞,
],最小值为-
.
所以
|
|
所以这个函数的解析式y=2x2-x-1;
(2)由(1)得y=2(x-
| 1 |
| 4 |
| 9 |
| 8 |
| 1 |
| 4 |
| 9 |
| 8 |
| 1 |
| 4 |
(3)由(2)得y=2(x-
| 1 |
| 4 |
| 9 |
| 8 |
| 1 |
| 4 |
| 1 |
| 4 |
| 9 |
| 8 |
点评:本题考查了二次函数得解析式求法以及单调区间和最值求法;利用待定系数法求函数解析式时常用方法,求二次函数得单调区间和最值通常配方,属于基础题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
已知P={-1,0,
},Q={y|y=sinθ,θ∈R},则P∩∁RQ=( )
| 2 |
| A、∅ | ||
B、{
| ||
| C、{-1,0} | ||
D、{-1,0,
|
下列结论错误的是( )
| A、命题:“若a>b>0,则a2>b2”的逆命题是假命题 | ||||||||
| B、若函数f(x)可导,则f′(x0)是x0为函数极值点的必要不充分条件 | ||||||||
C、向量
| ||||||||
| D、命题p:“?x∈R,ex≥x+1”的否定是“?x∈R,ex<x+1” |
如果双曲线的a=2,一个焦点为(5,0),则其标准方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
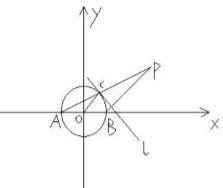 已知A,B是⊙0:x2+y2=4与x轴的两个交点,C是⊙O上异于点A,B的任意一点,过点B作直线l的垂线BP,且与AC的延长线交于点P,求点P的轨迹方程.
已知A,B是⊙0:x2+y2=4与x轴的两个交点,C是⊙O上异于点A,B的任意一点,过点B作直线l的垂线BP,且与AC的延长线交于点P,求点P的轨迹方程.