题目内容
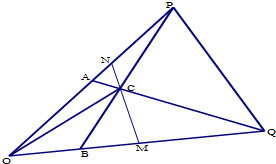
在△OPQ中，
=
，
=
，QA与PB相交于点C，设
=
，
=
（1）用
，
表示
；
（2）过C点作直线l分别与线段OQ，OP交于点M，N，设
=λ
，
=μ
，求证：
+
=1．
| OA |
| 1 |
| 2 |
| OP |
| OB |
| 1 |
| 3 |
| OQ |
| OP |
| a |
| OQ |
| b |
（1）用
| a |
| b |
| OC |
（2）过C点作直线l分别与线段OQ，OP交于点M，N，设
| OM |
| OQ |
| ON |
| OP |
| 2 |
| 5μ |
| 1 |
| 5λ |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：（1）由A，C，Q三点共线可得，存在t使：
=k
，这样便容易得到，
=
+k
；同理可得到存在t使：
=t
+
，根据平面向量基本定理便得，
，这样即可求出k，t，从而用
，
表示出
；
（2）由N，C，M三点共线可得，存在x使：
=x
+(1-x)
=xλ
+(1-x)μ
，又由（1）知
=
+
，所以
，这样即可求出
+
=1．
| AC |
| AQ |
| OC |
| 1-k |
| 2 |
| a |
| b |
| OC |
| a |
| 1-t |
| 3 |
| b |
|
| a |
| b |
| OC |
（2）由N，C，M三点共线可得，存在x使：
| OC |
| OM |
| ON |
| b |
| a |
| OC |
| 2 |
| 5 |
| a |
| 1 |
| 5 |
| b |
|
| 2 |
| 5μ |
| 1 |
| 5λ |
解答：
解：（1）∵A，C，Q三点共线，∴存在实数k，使
=k
，∴
=k
+(1-k)
=
+k
；
同理，P，C，B三点共线，∴得到存在实数t，使
=t
+(1-t)
=t
+
；
∴根据平面向量基本定理知：
，解得k=
，t=
；
∴
=
+
；
（2）由N，C，M三点共线，
=x
+(1-x)
=xλ
+(1-x)μ
；
又由（1）知
=
+
所以
，∴
+
=1-x+x=1．
| AC |
| AQ |
| OC |
| OQ |
| OA |
| 1-k |
| 2 |
| a |
| b |
同理，P，C，B三点共线，∴得到存在实数t，使
| OC |
| OP |
| OB |
| a |
| 1-t |
| 3 |
| b |
∴根据平面向量基本定理知：
|
| 1 |
| 5 |
| 2 |
| 5 |
∴
| OC |
| 2 |
| 5 |
| a |
| 1 |
| 5 |
| b |
（2）由N，C，M三点共线，
| OC |
| OM |
| ON |
| b |
| a |
又由（1）知
| OC |
| 2 |
| 5 |
| a |
| 1 |
| 5 |
| b |
所以
|
| 2 |
| 5μ |
| 1 |
| 5λ |
点评：考查共线向量基本定理，平面向量基本定理．
练习册系列答案
相关题目
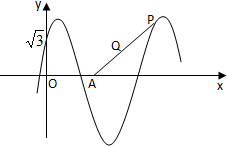如图所示，函数y=2sin（ωx+ϕ）（x∈R，ω＞0，0≤ϕ≤