题目内容
数列{an}的各项均为正数,Sn为其前n项和,对于任意n∈N*,总有2Sn=an2+an.
(1)求数列{an}的通项公式;
(2)求数列{an(
)n}的前n项和.
(1)求数列{an}的通项公式;
(2)求数列{an(
| 1 |
| 2 |
考点:数列的求和
专题:综合题,等差数列与等比数列
分析:(1)由已知可得2Sn-1=an-1+an-12(n≥2从而导出an+an-1=(an+an-1)(an-an-1)∵an,an-1均为正数,所以an-an-1=1(n≥2),由此推出an=n.
(2)利用错位相减法即可求得数列{an(
)n}的前n项和.
(2)利用错位相减法即可求得数列{an(
| 1 |
| 2 |
解答:
解:(1)由已知:对于n∈N*,总有2Sn=an+an2①成立
∴2Sn-1=an-1+an-12(n≥2)②
①②得2an=an+an2-an-1-an-12
∴an+an-1=(an+an-1)(an-an-1)∵an,an-1均为正数,
∴an-an-1=1(n≥2)
∴数列{an}是公差为1的等差数列又n=1时,2S1=a1+a12,解得a1=1.
∴an=n.
(2)Sn=1×
+2×(
)2+…+n•(
)n①
∴
Sn=1×(
)2+2×(
)3+…+(n-1)×(
)n+n•(
)n+1②
①-②得sn=2-
-n•
.
∴2Sn-1=an-1+an-12(n≥2)②
①②得2an=an+an2-an-1-an-12
∴an+an-1=(an+an-1)(an-an-1)∵an,an-1均为正数,
∴an-an-1=1(n≥2)
∴数列{an}是公差为1的等差数列又n=1时,2S1=a1+a12,解得a1=1.
∴an=n.
(2)Sn=1×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
①-②得sn=2-
| 1 |
| 2n-1 |
| 1 |
| 2n |
点评:本题考查数列的求和,着重考查等差数列的判定及其通项公式的应用,突出考查错位相减法求和,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
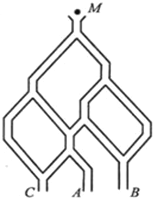 如图,一个小球从 M处投入,通过管道自上而下落A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C,则分别设为l,2,3等奖.
如图,一个小球从 M处投入,通过管道自上而下落A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C,则分别设为l,2,3等奖.