题目内容
已知sinα+cosα=
,
<α<π,求sinα-cosα的值.
| ||
| 3 |
| π |
| 2 |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:利用同角三角函数基本关系式、三角函数的单调性即可得出.
解答:
解:∵sinα+cosα=
,
∴sin2α+cos2α+2sinαcosα=
,
可得2sinαcosα=-
.
∴(sinα-cosα)2=1-2sinαcosα=
.
∵
<α<π,
∴sinα>0,cosα<0.
∴sinα-cosα=
.
| ||
| 3 |
∴sin2α+cos2α+2sinαcosα=
| 2 |
| 9 |
可得2sinαcosα=-
| 7 |
| 9 |
∴(sinα-cosα)2=1-2sinαcosα=
| 23 |
| 9 |
∵
| π |
| 2 |
∴sinα>0,cosα<0.
∴sinα-cosα=
| ||
| 3 |
点评:本题考查了同角三角函数基本关系式、三角函数的单调性,属于基础题.

练习册系列答案
相关题目
阅读如图所示的程序框图,若输入的x=4,则运行该程序后输出的实数y等于( )


| A、1 | B、2 | C、4 | D、9 |
若点M是△ABC所在平面内的一点,且满足|3
-
-
|=0,则△ABM与△ABC面积之比等于( )
| AM |
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法正确的是( )
| A、命题“若x2=1,则x=1”的否命题是“若x2=1,则x≠1” |
| B、命题“x∈R,x2-x>0”的否定是“x∈R,x2-x<0” |
| C、命题“若函数f(x)=x2-ax+1有零点,则a≥2或a≤-2”的逆否命题为真命题 |
| D、“x=-1”是“x2-x-2=0”的必要不充分条件 |
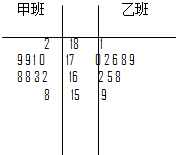 最近我校对高一学生进行了体检,为了了解甲乙两班男生的身高状况,随机从甲乙两班中各抽取10名男生的身高(单位cm),绘制身高的茎叶图如图:
最近我校对高一学生进行了体检,为了了解甲乙两班男生的身高状况,随机从甲乙两班中各抽取10名男生的身高(单位cm),绘制身高的茎叶图如图: 如图,在边长为1的正方形中随机撒1000粒豆子,有230粒落在阴影部分,据此估计阴影部分的面积为
如图,在边长为1的正方形中随机撒1000粒豆子,有230粒落在阴影部分,据此估计阴影部分的面积为