题目内容
设数列{an}的各项为正数,前n项和为Sn,且2
=an+1(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)记bn=
,若b1+b2+…+bn>1,求正整数n的最小值.
| Sn |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)记bn=
| 1 | ||||
|
考点:数列的求和,数列的函数特性
专题:等差数列与等比数列
分析:(Ⅰ)利用公式法可得an+1-an=2,数列{an}是等差数列,即可写出通项公式;
(Ⅱ)由(Ⅰ)得bn=
=
.利用裂项相消法求数列和,即可解得结论.
(Ⅱ)由(Ⅰ)得bn=
| 1 | ||||
|
| ||||
| 2 |
解答:
解:(Ⅰ)由2
=an+1,平方得4sn=(an+1)2,∴4sn+1=(an+1+1)2.
两式相减得4an+1=(an+1+1)2-(an+1)2,整理得(an+1-1)2-(an+1)2=0,
即(an+1+an)(an+1-an-2)=0.∵an>0,∴an+1-an-2=0,即an+1-an=2.
又∵当n=1时,2
=a1+1,(
-1)2=0,∴a1=1,
∴an=2n-1.
(Ⅱ)∵bn=
=
.
∴b1+b2+…+bn=
(
-1+
-
+…+
-
=
(
-1),
∴
(
-1)>1,解得n>4,
∴正整数n的最小值为5.
| Sn |
两式相减得4an+1=(an+1+1)2-(an+1)2,整理得(an+1-1)2-(an+1)2=0,
即(an+1+an)(an+1-an-2)=0.∵an>0,∴an+1-an-2=0,即an+1-an=2.
又∵当n=1时,2
| a1 |
| a1 |
∴an=2n-1.
(Ⅱ)∵bn=
| 1 | ||||
|
| ||||
| 2 |
∴b1+b2+…+bn=
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 2n+1 |
| 2n-1 |
| 1 |
| 2 |
| 2n+1 |
∴
| 1 |
| 2 |
| 2n+1 |
∴正整数n的最小值为5.
点评:本题主要考查数列通项公式的求法及裂项相消法求数列的和等知识,考查学生的分析问题、解决问题的能力及运算求解能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
直线x-y+2=0的倾斜角为( )
| A、60° | B、120° |
| C、45° | D、135° |
阅读如图所示的程序框图,若输入的x=4,则运行该程序后输出的实数y等于( )


| A、1 | B、2 | C、4 | D、9 |
函数f(x)=-2x2-x+1,x∈[-3,1]的最大值与最小值的和为( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|
若点M是△ABC所在平面内的一点,且满足|3
-
-
|=0,则△ABM与△ABC面积之比等于( )
| AM |
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
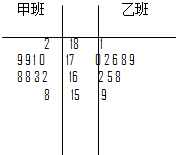 最近我校对高一学生进行了体检,为了了解甲乙两班男生的身高状况,随机从甲乙两班中各抽取10名男生的身高(单位cm),绘制身高的茎叶图如图:
最近我校对高一学生进行了体检,为了了解甲乙两班男生的身高状况,随机从甲乙两班中各抽取10名男生的身高(单位cm),绘制身高的茎叶图如图: