题目内容

已知向量
a
与
b
同向，
b
=（1，2），
a
•
b
=10．
（1）求向量
a
的坐标；
（2）若
c
=（2，-1），求（
b
•
c
）•
a
．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（1）设
a
=k
b
=（k，2k），（k＞0），利用
a
•
b
=10，解得k即可得出．
（2）利用数量积运算、数乘运算即可得出．
解答： 解：（1）设
a
=k
b
=（k，2k），（k＞0），
∵
a
•
b
=10，∴k+4k=10，解得k=2．
∴
a
=（2，4）．
（2）∵
c
=（2，-1），
∴
b
•
c
=2-2=0，
∴（
b
•
c
）•
a
=0×
a
=
0
．
点评：本题考考查了向量的数量积运算、数乘运算、向量共线定理，属于基础题．
练习册系列答案
相关题目
若f（x）=a+bsinx（b＜0）的最大值为
3
2
，最小值为-
1
2
，求：
（1）f（x）的解析式；
（2）在区间（0，2π）内使f（x）=0的x值．
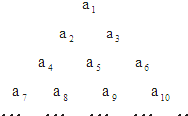已知数列{an}，an=3•(
1
2
)n-1，把数列{an}的各项排成三角形状，如图所示．记A（m，n）表示第m行，第n列的项，则A（10，8）=（　　）
A、3•(
1
2
)17
B、3•(
1
2
)50
C、3•(
1
2
)53
D、3•(
1
2
)52
已知|
a
|=2，|
b
|=2，且向量
a
在向量
b
的方向上的投影为-1．
（1）求向量
a
与
b
的夹角θ的值；
（2）求（
a
-2
b
）•
b
的值．
在四边形ABCD中，
AC
=（1，1），
BD
=（-2，3），则该四边形的面积为
 
．
定义运算：
.
ab
cd
.
=ad-bc，若方程
.
3
cosx		sinx
cosxcosx
.
=
3
2
，x∈（3，4），则实数x的值为
 
．
探究函数y=x 
2
3
的性质：
（1）指出函数的定义域和值域；
（2）判断函数的奇偶性；
（3）指出函数的递增区间和递减区间．
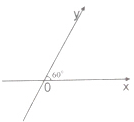如图所示，∠xoy=60°，
e1
，
e2
，分别是与x轴、y轴正方向相同的单位向量，若
m
=x
e1
+y
e2
，记
m
=（x，y），设
a
=（p，q），若
a
的模长为1，则p+q的最大值是（　　）
A、1
B、
2
3
3
C、C
2
2
D、
4
3
已知命题p：x2-2x-2≥1；命题q：0＜x＜4，若“p∨q”为真．“p∧q”为假．求实数x的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网