题目内容
已知不恒为零的函数f(x)对任意实数x,y满足f(x+y)+f(x-y)=2f(x)+2f(y),则函数f(x)为 函数.
考点:抽象函数及其应用
专题:函数的性质及应用
分析:我们可以得到设x=y=0,则f(0)=0,再令x=0,y=x得f(x)=f(-x),进而根据函数奇偶性的定义得到结论f(x)为偶函数,
解答:
解:∵不恒为零的函数f(x)对任意实数x,y满足f(x+y)+f(x-y)=2f(x)+2f(y),
令x=y=0,
则f(0)+f(0)=2f(0)+2f(0),
∴f(0)=0,
再令x=0,y=x
则f(x)+f(-x)=2f(0)+2f(x),
∴f(x)=f(-x),
∴f(x)为偶函数.
故答案为:偶.
令x=y=0,
则f(0)+f(0)=2f(0)+2f(0),
∴f(0)=0,
再令x=0,y=x
则f(x)+f(-x)=2f(0)+2f(x),
∴f(x)=f(-x),
∴f(x)为偶函数.
故答案为:偶.
点评:本题考查的知识点是抽象函数,赋值法是解决抽象函数的常用方法,属于基础题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
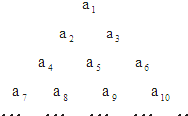 已知数列{an},an=3•(
已知数列{an},an=3•(| 1 |
| 2 |
A、3•(
| ||
B、3•(
| ||
C、3•(
| ||
D、3•(
|
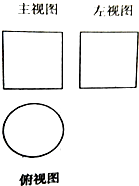 如图一个空间几何体的主视图和左视图都是边长为2的正方形,俯视图是一个圆,则该几何体的侧面积为
如图一个空间几何体的主视图和左视图都是边长为2的正方形,俯视图是一个圆,则该几何体的侧面积为