题目内容
已知函数f(x)=x3-ax,g(x)=
x2-lnx-
.
(Ⅰ)若f(x)在x=1处的切线与x轴平行,求实数a的值;
(Ⅱ)若对一切x∈(0,+∞),有不等式f(x)≥2x•g(x)-x2+5x-3恒成立,求实数a的取值范围;
(Ⅲ)记G(x)=
x2-
-g(x),求证:G(x)>
-
.
| 1 |
| 2 |
| 5 |
| 2 |
(Ⅰ)若f(x)在x=1处的切线与x轴平行,求实数a的值;
(Ⅱ)若对一切x∈(0,+∞),有不等式f(x)≥2x•g(x)-x2+5x-3恒成立,求实数a的取值范围;
(Ⅲ)记G(x)=
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| ex |
| 2 |
| ex |
考点:利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题:综合题,导数的概念及应用
分析:(Ⅰ)若f(x)在x=1处的切线与x轴平行,f(x) 在x=1处的切线斜率为0,即可求实数a的值;
(Ⅱ)原不等式可化为a≤(2lnx+
+x)min.
(Ⅲ)原不等式可化为lnx>
-
,即证xlnx>
-
成立,确定左边的最小值,右边的最大值,即可证明.
(Ⅱ)原不等式可化为a≤(2lnx+
| 3 |
| x |
(Ⅲ)原不等式可化为lnx>
| 1 |
| ex |
| 2 |
| ex |
| x |
| ex |
| 2 |
| e |
解答:
解:(Ⅰ)f′(x)=3x2-a,
∵f(x)在x=1处的切线与x轴平行,
∴f(x) 在x=1处的切线斜率为0
即f′(1)=3-a,∴a=3;
(Ⅱ)原不等式可化为:x3-ax≥2x(
x2-lnx-
)-x2+5x-3,
∵x>0,∴化简得:a≤(2lnx+
+x)min.
记t(x)=2lnx+
+x(x>0),则t′(x)=
令t′(x)=0,∵x>0,∴x=1,
∴在(0,1)上,t′(x)<0,在(1,+∞)上,t′(x)>0
∴t(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
故当x=1时,t(x)有最小值为4,故a∈(-∞,4];
(Ⅲ)化简得G(x)=lnx,原不等式可化为lnx>
-
,即证xlnx>
-
成立,
记F(x)=xlnx,可求其最小值为F(
)=-
,
记H(x)=
-
,可求其最大值为H(1)=-
,
显然x∈(0,+∞),F(x)>H(x),故原不等式成立.
∵f(x)在x=1处的切线与x轴平行,
∴f(x) 在x=1处的切线斜率为0
即f′(1)=3-a,∴a=3;
(Ⅱ)原不等式可化为:x3-ax≥2x(
| 1 |
| 2 |
| 5 |
| 2 |
∵x>0,∴化简得:a≤(2lnx+
| 3 |
| x |
记t(x)=2lnx+
| 3 |
| x |
| x2+2x-3 |
| x2 |
令t′(x)=0,∵x>0,∴x=1,
∴在(0,1)上,t′(x)<0,在(1,+∞)上,t′(x)>0
∴t(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
故当x=1时,t(x)有最小值为4,故a∈(-∞,4];
(Ⅲ)化简得G(x)=lnx,原不等式可化为lnx>
| 1 |
| ex |
| 2 |
| ex |
| x |
| ex |
| 2 |
| e |
记F(x)=xlnx,可求其最小值为F(
| 1 |
| e |
| 1 |
| e |
记H(x)=
| x |
| ex |
| 2 |
| e |
| 1 |
| e |
显然x∈(0,+∞),F(x)>H(x),故原不等式成立.
点评:本题考查导数知识的综合运用,考查导数的几何意义,考查函数的单调性与最值,考查不等式的证明,正确求导是关键.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
事件A,B的概率分别为p1,p2,且p1<p2则( )
| A、P(A∩B)<p1 |
| B、P(A∪B)>p2 |
| C、P(A∪B)=p2+p1 |
| D、以上都不正确 |
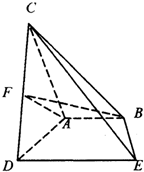 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点. 如图,在四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.
如图,在四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.