题目内容
椭圆
+
=1的焦点坐标为（ ）
| y2 |
| 13 |
| x2 |
| 4 |
| A、（±2，0） |
| B、（±3，0） |
| C、（0，±2） |
| D、（0，±3） |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：确定椭圆的
+
=1中a2=13，b2=4，求出c，即可求出椭圆的焦点坐标．
| y2 |
| 13 |
| x2 |
| 4 |
解答：
解：椭圆的
+
=1中a2=13，b2=4，
∴c2=a2-b2=9，又该椭圆焦点在y轴，
∴焦点坐标为：（0，±3）．
故选：D．
| y2 |
| 13 |
| x2 |
| 4 |
∴c2=a2-b2=9，又该椭圆焦点在y轴，
∴焦点坐标为：（0，±3）．
故选：D．
点评：本题考查椭圆的简单性质，利用c2=a2-b2是关键，属于基础题．
练习册系列答案
相关题目
设函数f（x）=3x+3x-8，用二分法求得方程f（x）=0在x∈（1，2）内的根所在的区间可以是（ ）
（参考数据：f（1.25）≈-0.30，f（1.5）≈1.70，f（1.75）≈4.09）
（参考数据：f（1.25）≈-0.30，f（1.5）≈1.70，f（1.75）≈4.09）
| A、（1，1.25） |
| B、（1.25，1.5） |
| C、（1.5，1.75） |
| D、（1.75，2） |
“（2x+1）x=0”是“x=0”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
椭圆
+
=1的一个焦点坐标是（ ）
| x2 |
| 3 |
| y2 |
| 4 |
| A、（1，0） |
| B、（0，1） |
| C、（0，7） |
| D、（7，0） |
已知an=n（n+1），以下四个数中，哪个是数列{an}中的一项（ ）
| A、18 | B、21 | C、25 | D、30 |
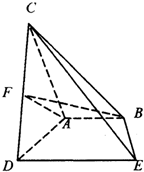如图，已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD=DE=2AB=2，F为CD的中点．