题目内容
从1开始的自然数按如图所示的规则排列，现有一个三角形框架在图中上下或左右移动，使每次恰有九个数在此三角形内，则这九个数的和可以为（ ）| A、2097 | B、1553 |
| C、1517 | D、2111 |
考点：进行简单的合情推理
专题：计算题,推理和证明
分析：设最上层的一个数为a，则第二层的三个数为a+7，a+8，a+9，第三层的五个数为a+14，a+15，a+16，a+17，a+18，根据题意求和验证．
解答：
解：根据如图所示的规则排列，设最上层的一个数为a，则第二层的三个数为a+7，a+8，a+9，第三层的五个数为a+14，a+15，a+16，a+17，a+18，
这9个数之和为a+3a+24+5a+80=9a+104．
由求出的a一定要在每行的第3，4，5，6个数，9a+104=1517，得a=157，是自然数．
故选C．
这9个数之和为a+3a+24+5a+80=9a+104．
由求出的a一定要在每行的第3，4，5，6个数，9a+104=1517，得a=157，是自然数．
故选C．
点评：此题考查数字的变化规律，利用表格中的数据特点进行简单的合情推理，得出9个数的关系是解决问题的关键．
练习册系列答案
口算能手系列答案
相关题目
极坐标方程ρcos2θ=0表示的曲线为（ ）
| A、极点 | B、两条相交直线 |
| C、一条直线 | D、极轴 |
设函数f（x）=3x+3x-8，用二分法求得方程f（x）=0在x∈（1，2）内的根所在的区间可以是（ ）
（参考数据：f（1.25）≈-0.30，f（1.5）≈1.70，f（1.75）≈4.09）
（参考数据：f（1.25）≈-0.30，f（1.5）≈1.70，f（1.75）≈4.09）
| A、（1，1.25） |
| B、（1.25，1.5） |
| C、（1.5，1.75） |
| D、（1.75，2） |
下面命题正确的个数是（ ）
（1）若直线l上有无数个点不在平面α内，则l∥α；
（2）若直线l平行于平面α内的无数条直线，则l∥α；
（3）若直线l与平面α平行，则l与平面α内的任一直线平行；
（4）若直线l在平面α外，则l∥α．
（1）若直线l上有无数个点不在平面α内，则l∥α；
（2）若直线l平行于平面α内的无数条直线，则l∥α；
（3）若直线l与平面α平行，则l与平面α内的任一直线平行；
（4）若直线l在平面α外，则l∥α．
| A、0个 | B、1个 | C、2个 | D、3个 |
如果在两个平面内分别有一条直线，这两条直线互相平行，那么这两个平面的位置关系一定是（ ）
| A、平行 | B、相交 |
| C、平行或相交 | D、垂直相交 |
事件A，B的概率分别为p1，p2，且p1＜p2则（ ）
| A、P（A∩B）＜p1 |
| B、P（A∪B）＞p2 |
| C、P（A∪B）=p2+p1 |
| D、以上都不正确 |
“（2x+1）x=0”是“x=0”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
椭圆
+
=1的一个焦点坐标是（ ）
| x2 |
| 3 |
| y2 |
| 4 |
| A、（1，0） |
| B、（0，1） |
| C、（0，7） |
| D、（7，0） |
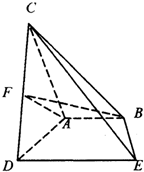如图，已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD=DE=2AB=2，F为CD的中点．