题目内容
18.已知不等式$\frac{a}{x-2}$>1-a(1)若a=x,求关于x不等式的解集;
(2)若a≠1,求关于x不等式的解集.
分析 (1)若a=x,根据分式不等式的解法,即可求关于x不等式的解集;
(2)若a≠1,讨论a的取值范围,即可求关于x不等式的解集.
解答 解:(1)a=x,则$\frac{x}{x-2}$>1-x,
∴$\frac{{{x^2}-2x+2}}{x-2}>0\\∵{x^2}-2x+2={({x-1})^2}+1>0$,∴$x>2\\∴原不等式的解集为\left\{{x\left|{x>2}\right.}\right\}\\(2)\frac{a}{x-2}>1-a?\frac{{({a-1})x-({a-2})}}{x-2}>0\end{array}$,故不等式的解集为(2,+∞),
(2)①a>1时,可转化为$({x-2})({x-\frac{a-2}{a-1}})>0$
此时$\frac{a-2}{a-1}<2$,不等式的解集为$\left\{{\left.x\right|x<\frac{a-2}{a-1}或x>2}\right\}$
②a<1时,可转化为$({x-2})({x-\frac{a-2}{a-1}})<0$
(i)当$\frac{a-2}{a-1}>2$即0<a<1时,不等式的解集为$\left\{{\left.x\right|2<x<\frac{a-2}{a-1}}\right\}$
(ii)当$\frac{a-2}{a-1}=2$即a=0时,不等式的解集为∅
(iii)当$\frac{a-2}{a-1}<2$即a<0时,不等式的解集为$\left\{{\left.x\right|\frac{a-2}{a-1}<x<2}\right\}$,
综上所述:当a>1时,解集为$\left\{{\left.x\right|x<\frac{a-2}{a-1}或x>2}\right\}$;
当0<a<1时,解集为$\left\{{\left.x\right|2<x<\frac{a-2}{a-1}}\right\}$;
当a=0时,不等式的解集为∅;
当a<0时,不等式的解集为$\left\{{\left.x\right|\frac{a-2}{a-1}<x<2}\right\}$.
点评 本题主要考查分式不等式的解法,利用分类讨论是解决本题的关键.

 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案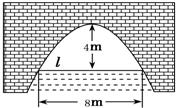 如图是抛物线形拱桥,当水面在l时,拱顶离水面4米,水面宽8米.水位上升1米后,水面宽为( )
如图是抛物线形拱桥,当水面在l时,拱顶离水面4米,水面宽8米.水位上升1米后,水面宽为( )| A. | $\sqrt{3}$米 | B. | $2\sqrt{3}$米 | C. | $3\sqrt{3}$米 | D. | $4\sqrt{3}$米 |
| A. | $\left\{\begin{array}{l}x=3cosθ\\ y=2sinθ\end{array}\right.(θ为参数)$ | B. | $\left\{\begin{array}{l}x=2cosθ\\ y=3sinθ\end{array}\right.(θ为参数)$ | ||
| C. | $\left\{\begin{array}{l}x=9cosθ\\ y=4sinθ\end{array}\right.(θ为参数)$ | D. | $\left\{\begin{array}{l}x=4cosθ\\ y=9sinθ\end{array}\right.(θ为参数)$ |