题目内容
10.A、B是抛物线y2=2px(p>0)上的两点,满足$\overrightarrow{OA}$•$\overrightarrow{OB}$=0(O是原点),求证:(1)A、B两点的横坐标之积,纵坐标之积均为定值.
(2)直线AB过定点.
分析 (1)OA⊥OB时,设直线AB:x=my+n,代入抛物线方程,可得y2-2pmy-2pn=0,利用OA⊥OB,即可证明A、B两点的横坐标之积为定值;
(2)由(1)知,直线AB:x=my+2p过定点(2p,0).
解答 证明:(1)OA⊥OB时,设直线AB:x=my+n.
代入抛物线方程,可得y2-2pmy-2pn=0,
∵OA⊥OB,
∴x1x2+y1y2=$\frac{({y}_{1}{y}_{2})^{2}}{4{p}^{2}}$+y1y2=0,
∴y1y2=-4p2=-2pn,
∴n=2p,
∴x1x2=4p2;
(2)由(1)知,直线AB:x=my+2p过定点(2p,0).
点评 本题考查抛物线方程,考查学生的计算能力,考查直线与抛物线的位置关系,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知圆C:x2+y2+2x-4y+3=0.
(1)直线l过点(-2,0)且被圆C截得的弦长为2,求直线l的方程;
(2)从直线2x-4y+3=0上一点P向圆引一条切线,切点为M,求|PM|的最小值.
(1)直线l过点(-2,0)且被圆C截得的弦长为2,求直线l的方程;
(2)从直线2x-4y+3=0上一点P向圆引一条切线,切点为M,求|PM|的最小值.
18.已知△ABC的三条边长为a,b,c,则“△ABC是等边三角形”是“a2+b2+c2=ab+ac+bc”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.若直线ax+by=1经过圆x2+y2=1内一点,则点(a,b)与此圆的位置关系是( )
| A. | 点在圆上 | B. | 点在圆内 | C. | 点在圆外 | D. | 都有可能 |
2.(x2-$\frac{3}{{x}^{3}}$)5的展开式中常数项为( )
| A. | 270 | B. | -270 | C. | -90 | D. | 90 |
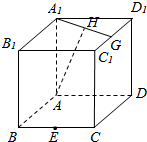 如图,棱长为1的正方体ABCD-A1B1C1D1中,E是BC的中点,F是棱CD上的动点,G为C1D&1的中点,H为A1G的中点.
如图,棱长为1的正方体ABCD-A1B1C1D1中,E是BC的中点,F是棱CD上的动点,G为C1D&1的中点,H为A1G的中点.