题目内容
2.椭圆的两个焦点和短轴的两个端点,恰好是含60°角的菱形的四个顶点,则椭圆的离心率为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$或$\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$或$\frac{\sqrt{3}}{3}$ |
分析 由题意可得tan30°=$\frac{c}{b}$,或tan60°=$\frac{c}{b}$,再由a,b,c的关系和离心率公式,计算即可得到所求值.
解答 解:由于椭圆的两个焦点和短轴两个顶点,
是一个含60°角的菱形的四个顶点,
则tan30°=$\frac{c}{b}$,或tan60°=$\frac{c}{b}$,
当$\frac{c}{b}$=$\frac{\sqrt{3}}{3}$时,即b=$\sqrt{3}$c,即有a=$\sqrt{{b}^{2}+{c}^{2}}$=2c,
由e=$\frac{c}{a}$=$\frac{1}{2}$;
当$\frac{c}{b}$=$\sqrt{3}$时,即b=$\frac{\sqrt{3}}{3}$c,即有a=$\sqrt{{b}^{2}+{c}^{2}}$=$\frac{2\sqrt{3}}{3}$c,
由e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$.
可得离心率为$\frac{1}{2}$或$\frac{\sqrt{3}}{2}$.
故选:C.
点评 本题考查椭圆的标准方程,以及简单性质的应用,运用分类讨论的思想方法是解题的关键.

练习册系列答案
相关题目
13.已知双曲线与椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{25}$=1共焦点,它们的离心率之和为$\frac{14}{5}$,双曲线的方程应是( )
| A. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 | C. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{12}$=1 | D. | $\frac{{y}^{2}}{12}$-$\frac{{x}^{2}}{4}$=1 |
10.已知条件p:x2-3x+2<0;条件q:|x-2|<1,则p是q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
17.设P是焦距为6的双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)右支上一点,双曲线C的一条渐近线与圆(x-3)2+y2=5相切,若P到两焦点距离之和为8,则P到两焦点距离之积为( )
| A. | 6 | B. | 6$\sqrt{2}$ | C. | 10 | D. | 12 |
7.设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,P是椭圆上一点,|PF1|=2|PF2|,∠F1PF2=$\frac{π}{3}$,则椭圆离心率的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
11.执行如图所示的程序框图,则输出的S的值是( )
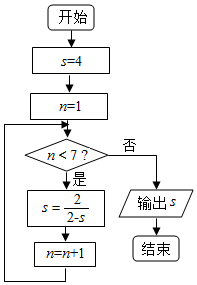

| A. | -1 | B. | 4 | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
12.在复平面内,复数(1-2i)2对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |