题目内容
7．用总长为14.8m的钢条制作一个长方体容器的框架，若所制作容器的底面一边比高长出0.5m，则当高为1m时，容器的容积最大．分析 将容器容积表示成高x的函数关系，然后利用导数求此函数的最值，注意如何选择自变量．
解答 解：设容器高为xm，则底面一边长为（x+0.5）m，另一边长为3.2-2x．
由3.2-2x＞0和x＞0，得0＜x＜1.6，
设容器的容积为ym3，
则有y=x（x+0.5）（3.2-2x），（0＜x＜1.6）．
整理，得y=-2x3+2.2x2+1.6x，
∴y′=-6x2+4.4x+1.6．
令 y′=0，有x=1．
从而在定义域（0，1.6）内只有在x=1处使y取最大值，
故答案为：1．
点评 本小题主要考查应用所学导数的知识、思想和方法解决实际问题的能力，建立函数式、解方程、不等式、最大值等基础知识．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
17．设P是焦距为6的双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）右支上一点，双曲线C的一条渐近线与圆（x-3）2+y2=5相切，若P到两焦点距离之和为8，则P到两焦点距离之积为（ ）
| A． | 6 | B． | 6$\sqrt{2}$ | C． | 10 | D． | 12 |
18．一个多面体的三视图如图所示，则该多面体的体积为（ ）
| A． | 9 | B． | 15 | C． | 18 | D． | 21 |
15．已知直线方程为x+y+1=0，则该直线的倾斜角为（ ）
| A． | 45° | B． | 60° | C． | 90° | D． | 135° |
2．已知长方体ABCD-A1B1C1D1的体积为1，则四面体AB1CD1与四面体A1BC1D重叠部分的体积是（ ）
| A． | $\frac{1}{8}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
12．在复平面内，复数（1-2i）2对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
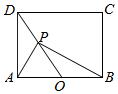如图在长方形ABCD中，$AB=2\sqrt{2}$，AD=2，O为AB的中点，若P是线段DO上动点，则（$\overrightarrow{PA}$+$\overrightarrow{PB}$）•$\overrightarrow{PD}$的最小值是-3．
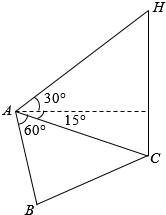为了应对日益严重的气候问题，某气象仪器科研单位研究出一种新的弹射型气象仪器，这种仪器可以弹射到空中进行气象观测．如图所示，假设这种仪器在C地进行弹射实验，在A，B两地进行观察弹射效果．已知A、B两地相距100米，∠BAC=60°在A地听到弹射声音的时间比B地晚$\frac{2}{17}$秒（已知声音在该地的传播速度为340米/秒），在A地测得该仪器在C处时的俯角为15°，A地测得该仪器至最高点H处的仰角为30°．