题目内容
3.已知函数f(x)=$\sqrt{x-3}$-$\frac{1}{\sqrt{7-x}}$的定义域为集合A.且B={x∈Z|2<x<10},C={x∈R|x<a或x>a+1}.(Ⅰ)求A和(∁UA)∩B;
(Ⅱ)若A∪C=R,求实数a的取值范围.
分析 (Ⅰ)根据f(x)的解析式,列出使解析式有意义的不等式组,求出解集A,再求∁RA∩B;
(Ⅱ)根据A∪C=R,列出不等式组$\left\{\begin{array}{l}{a≥3}\\{a+1<7}\end{array}\right.$,求出a的取值范围.
解答 解:(Ⅰ)∵f(x)=$\sqrt{x-3}$-$\frac{1}{\sqrt{7-x}}$,
∴$\left\{\begin{array}{l}{x-3≥0}\\{7-x>0}\end{array}\right.$,
解得3≤x<7,
∴A={x|3≤x<7};
∴∁RA={x|x<3或x≥7},
又B={x∈Z|2<x<10}={3,4,5,6,7,8,9},
∴∁RA∩B={7,8,9};
(Ⅱ)∵A={x|3≤x<7},C={x∈R|x<a或x>a+1},
且A∪C=R,
∴$\left\{\begin{array}{l}{a≥3}\\{a+1<7}\end{array}\right.$,
解得3≤a<6.
点评 本题考查了求函数的定义域以及集合的基本运算问题,是基础题.

练习册系列答案
相关题目
13.已知双曲线与椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{25}$=1共焦点,它们的离心率之和为$\frac{14}{5}$,双曲线的方程应是( )
| A. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 | C. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{12}$=1 | D. | $\frac{{y}^{2}}{12}$-$\frac{{x}^{2}}{4}$=1 |
11.执行如图所示的程序框图,则输出的S的值是( )
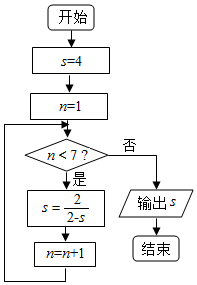

| A. | -1 | B. | 4 | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
18.一个多面体的三视图如图所示,则该多面体的体积为( )


| A. | 9 | B. | 15 | C. | 18 | D. | 21 |
15.已知直线方程为x+y+1=0,则该直线的倾斜角为( )
| A. | 45° | B. | 60° | C. | 90° | D. | 135° |
12.在复平面内,复数(1-2i)2对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.下列函数中,既是偶函数又在(0,+∞)上单调递增的是( )
| A. | y=ln|x| | B. | y=$\sqrt{{x}^{2}-1}$ | C. | y=sinx | D. | y=cosx |
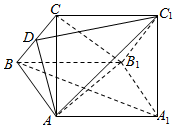 如图,三棱柱ABC-A1B1C1的侧面AA1B1B为正方形,侧面BB1C1C菱形,∠CBB1=60°,AB⊥平面BB1C1C,且D是BC的中点.
如图,三棱柱ABC-A1B1C1的侧面AA1B1B为正方形,侧面BB1C1C菱形,∠CBB1=60°,AB⊥平面BB1C1C,且D是BC的中点.