题目内容
已知函数f(x)=
x3-3x2+ax(a∈R)的所有切线中,有且仅有一条切线l与直线y=x垂直.
(1)求a的值和切线l的方程;
(2)设曲线y=f(x)在任一点处的切线倾斜角为α,求α的取值范围.
| 1 |
| 3 |
(1)求a的值和切线l的方程;
(2)设曲线y=f(x)在任一点处的切线倾斜角为α,求α的取值范围.
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:(1)由已知可得函数的导函数,即切线斜率的函数,因为在曲线y=f(x)的所有切线中,有且仅有一条切线l与直线y=x垂直,所以导函数只有一个实根,进而易得a的值与切线1的方程.
(2)因为在曲线y=f(x)的所有切线中,有且仅有一条切线l与直线y=x垂直,显然切线斜率≥-1从而可以解出θ的范围.
(2)因为在曲线y=f(x)的所有切线中,有且仅有一条切线l与直线y=x垂直,显然切线斜率≥-1从而可以解出θ的范围.
解答:
解:(1)∵f(x)=
x3-3x2+ax(a∈R),
∴f′(x)=x2-6x+a.
∵在曲线y=f(x)的所有切线中,有且仅有一条切线l与直线y=x垂直,
∴x2-6x+a=-1有且只有一个实数根.
∴△=36-4(a+1)=0,
∴a=8.
∴x=3,f(3)=6.即切点(3,6).
∴切线l:y-6=-(x-3),即x+y-3=0.
(2)∵f′(x)=x2-6x+8=(x-3)2-1≥-1.
∴tanα≥-1,
∵α∈[0,π),
∴α的取值范围是[0,
)∪[
,π).
| 1 |
| 3 |
∴f′(x)=x2-6x+a.
∵在曲线y=f(x)的所有切线中,有且仅有一条切线l与直线y=x垂直,
∴x2-6x+a=-1有且只有一个实数根.
∴△=36-4(a+1)=0,
∴a=8.
∴x=3,f(3)=6.即切点(3,6).
∴切线l:y-6=-(x-3),即x+y-3=0.
(2)∵f′(x)=x2-6x+8=(x-3)2-1≥-1.
∴tanα≥-1,
∵α∈[0,π),
∴α的取值范围是[0,
| π |
| 2 |
| 3π |
| 4 |
点评:本题主要考查导数的几何意义,同时考查了直线的点斜式方程及直线的倾斜角,是一道综合题,应注意运用导函数求解.

练习册系列答案
相关题目
若点P在
的终边上,且|OP|=2(O为坐标原点),则点P的坐标( )
| 2π |
| 3 |
A、(1,
| ||
B、(
| ||
C、(-1,-
| ||
D、(-1,
|
某几何体的三视图如图,其正视图中的曲线部分为半个圆弧,则该几何体的表面积为( )
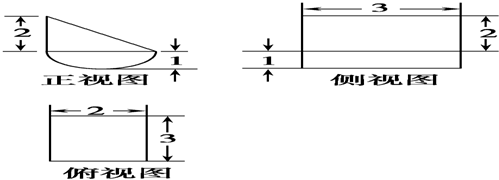

A、16+6
| ||
B、16+6
| ||
C、10+6
| ||
D、10+6
|
以下说法正确的是( )
| A、{0}是空集 |
| B、方程x2-3x=0的根为自然数 |
| C、{x∈N|x2-9≤0}是无限集 |
| D、空集是任何集合的真子集 |
已知点P(x0,y0)式抛物线y=3x2+6x+1上一点,且f′(x0)=0,则P点坐标为( )
| A、(1,10) |
| B、(-1,-2) |
| C、(1,-2) |
| D、.(-1,10) |