题目内容
设函数f(x)=loga(2x+1)在区间(-
,0)上满足f(x)>0.
(1)求实数a的取值范围;
(2)求函数f(x)的单调区间;
(3)解不等式f(x)>1.
| 1 |
| 2 |
(1)求实数a的取值范围;
(2)求函数f(x)的单调区间;
(3)解不等式f(x)>1.
考点:指、对数不等式的解法,复合函数的单调性
专题:函数的性质及应用
分析:(1)先把2x+1的范围求出来,从而确定a的取值范围;
(2)由(1)知a的范围,求单调区间;
(3)由对数的性质解不等式.
(2)由(1)知a的范围,求单调区间;
(3)由对数的性质解不等式.
解答:
解:(1)因为x∈(-
,0),
所以0<2x+1<1,
又f(x)>0,
故0<a<1.
(2)因0<a<1,
故函数的单调递减区间为(-
,+∞);
(3)f(x)=loga(2x+1)>1,又因0<a<1,
所以0<2x+1<a,
解得:-
<x<
,
所以原不等式的解集是:{x|:-
<x<
}.
| 1 |
| 2 |
所以0<2x+1<1,
又f(x)>0,
故0<a<1.
(2)因0<a<1,
故函数的单调递减区间为(-
| 1 |
| 2 |
(3)f(x)=loga(2x+1)>1,又因0<a<1,
所以0<2x+1<a,
解得:-
| 1 |
| 2 |
| a-1 |
| 2 |
所以原不等式的解集是:{x|:-
| 1 |
| 2 |
| a-1 |
| 2 |
点评:本题主要考查对数的性质,最好利用图象进行求解,属于基础题.

练习册系列答案
相关题目
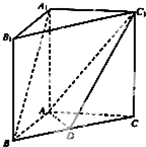 如图,在直三棱柱ABC-A1B1C1中,点D是BC的中点.
如图,在直三棱柱ABC-A1B1C1中,点D是BC的中点.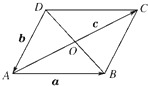 如图所示,O是平行四边形ABCD的对角线AC,BD的交点,设
如图所示,O是平行四边形ABCD的对角线AC,BD的交点,设