题目内容

讨论函数f（x）=
1
x-a
的单调性并证明．
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：通过求导得到函数的导数为负，结合函数的定义域求出单调区间．
解答： 解：∵f（x）=
1
x-a
，
∴f′（x）=-
1
(x-a)2
＜0，
∴f（x）在（-∞，a）递减，在（a，+∞）递减．
点评：本题考查了函数的单调性的判断，通过求导是常用的方法之一，本题属于基础题．
练习册系列答案
相关题目
已知函数y=x2-2x+2，求函数的值域．
分析g（x）=
x2+4
x
的大致图象，并求其最值．
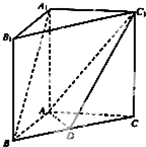如图，在直三棱柱ABC-A1B1C1中，点D是BC的中点．
（1）求证：A1B∥平面ADC1；
（2）若AB⊥AC，AB=AC=1，AA1=2，求平面ADC1与ABA1所成二面角的正弦值．
（1）已知等差数列{an}中，已知a1+a6=12，a4=7，求a9；
（2）已知等比数列{bn]中，b5=8，b7=2，bn＞0，求bn．
定义在D上的函数f（x），如果满足：对任意x∈D，存在常数M≥0，都有|f（x）|≤M成立，则称f（x）是D上的有界函数，其中M称为函数f（x）的一个上界．已知函数f(x)=1+a(
1
2
)x+(
1
4
)x，g(x)=log
1
2
1-ax
x-1
．
（1）若函数g（x）为奇函数，求实数a的值；
（2）若a=-1，判断g（x）在区间[
5
3
，3]上的单调性（不必证明），并求g（x）上界的最小值；
（3）若函数f（x）在[0，+∞）上是以3为上界的有界函数，求实数a的取值范围．
已知函数f(x)=cos2(x+
π
12
)，g（x）=1+
1
2
sin2x．
（1）设x0是函数y=f（x）的零点，求x0及g（x0）的值；
（2）求函数h（x）=f（x）+g（x）的单调递增区间．
已知圆x2+y2+6x-4=0，x2+y2+6y-28=0．求：
（1）公共弦长；
（2）它们的公共弦所在直线的方程．
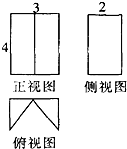如图，是一个几何体的正视图、侧视图、俯视图，且正视图、侧视图都是矩形，则该几何体的体积是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网