题目内容
已知双曲线
-
=1(a>0,b>0)中,若以其焦点为圆心,半实轴长为半径的圆与渐近线相切,则其渐近线方程为 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设出双曲线的焦点F和渐近线方程,利用圆心F到渐近线的距离是d=r,求出a与b的关系,即得渐近线方程.
解答:
解:设双曲线的焦点为F(c,0),渐近线方程为y=±
x,
化为直线的一般形式为bx±ay=0;
∴圆心F(c,0)到渐近线的距离是:
d=
=a;
即
=a,
∴a=b;
∴渐近线方程为y=±x.
故答案为:y=±x.
| b |
| a |
化为直线的一般形式为bx±ay=0;
∴圆心F(c,0)到渐近线的距离是:
d=
| bc | ||
|
即
| bc |
| c |
∴a=b;
∴渐近线方程为y=±x.
故答案为:y=±x.
点评:本题考查了双曲线的标准方程与几何性质的应用问题,也考查了点到直线的距离的应用问题,是基础题.

练习册系列答案
相关题目
设△ABC的内角A,B,C所对的边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为 ( )
| A、直角三角形 | B、锐角三角形 |
| C、钝角三角形 | D、不确定 |
对于任意x∈R,同时满足条件f(x)=f(-x)和f(x-π)=f(x)的函数是( )
| A、f(x)=sinx |
| B、f(x)=sinxcosx |
| C、f(x)=cosx |
| D、f(x)=cos2x-sin2x |
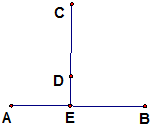 如图,某山区的两个工厂A、B直线距离14km,工厂C距A、B直线距离都是25km,E为线段AB的中点,在线段CE上选建变电站D,并从点D处铺设到工厂A,B,C的输电线DA,DB,DC.
如图,某山区的两个工厂A、B直线距离14km,工厂C距A、B直线距离都是25km,E为线段AB的中点,在线段CE上选建变电站D,并从点D处铺设到工厂A,B,C的输电线DA,DB,DC.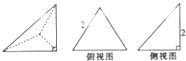 已知三棱锥的直观图及其俯视图与侧视图如图,俯视图是边长为2的正三角形,侧视图是有一直角边为2的直角三角形,则该三棱锥的正视图面积为( )
已知三棱锥的直观图及其俯视图与侧视图如图,俯视图是边长为2的正三角形,侧视图是有一直角边为2的直角三角形,则该三棱锥的正视图面积为( )