题目内容
已知三棱锥S-ABC的所有顶点都在球O的球面上,O为SC的中点,且SC=6,AB=2,∠ASC=∠BSC=30°,则此棱锥的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:设球心为点O,作AB中点D,连接OD,CD,说明SC是球的直径,利用余弦定理,三角形的面积公式求出S△SCD,和棱锥的高AB,即可求出棱锥的体积.
解答:
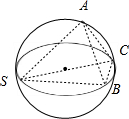 解:作AB中点D,连接OD,CD
解:作AB中点D,连接OD,CD
因为线段SC是球的直径,
所以它也是大圆的直径,则易得:∠SAC=∠SBC=90°
所以在Rt△SAC中,SC=6,∠ASC=30° 得:AC=3,SA=3
又在Rt△SBC中,SC=6,∠BSC=30° 得:BC=3,SB=3
则:SA=SB,AC=BC
因为点D是AB的中点,
所以在等腰三角形ASB中,SD⊥AB且SD=
=
在等腰三角形CAB中,CD⊥AB且CD=
=2
又SD交CD于点D
所以:AB⊥平面SCD
所以棱锥S-ABC的体积:V=
AB•S△SCD,
因为:SD=
,CD=2
,SC=6
所以由余弦定理得:cos∠SDC=
=-
则:sin∠SDC=
由三角形面积公式得△SCD的面积S=
SD•CD•sin∠SDC=
×
×2
×
=
所以:棱锥S-ABC的体积:V=
AB•S△SCD=
×2×
=
.
故选D.
 解:作AB中点D,连接OD,CD
解:作AB中点D,连接OD,CD 因为线段SC是球的直径,
所以它也是大圆的直径,则易得:∠SAC=∠SBC=90°
所以在Rt△SAC中,SC=6,∠ASC=30° 得:AC=3,SA=3
| 3 |
又在Rt△SBC中,SC=6,∠BSC=30° 得:BC=3,SB=3
| 3 |
则:SA=SB,AC=BC
因为点D是AB的中点,
所以在等腰三角形ASB中,SD⊥AB且SD=
| SA2-AD2 |
| 26 |
在等腰三角形CAB中,CD⊥AB且CD=
| AC2-AD2 |
| 2 |
又SD交CD于点D
所以:AB⊥平面SCD
所以棱锥S-ABC的体积:V=
| 1 |
| 3 |
因为:SD=
| 26 |
| 2 |
所以由余弦定理得:cos∠SDC=
| 26+8-36 | ||||
2×
|
| 1 | ||
4
|
则:sin∠SDC=
| ||
4
|
由三角形面积公式得△SCD的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 26 |
| 2 |
| ||
4
|
3
| ||
| 2 |
所以:棱锥S-ABC的体积:V=
| 1 |
| 3 |
| 1 |
| 3 |
3
| ||
| 2 |
| 23 |
故选D.
点评:本题是中档题,考查球的内接棱锥的体积的求法,考查空间想象能力,计算能力,有难度的题目,常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中,点M是AB的中点,N点分AC的比为AN:NC=1:2,BN与CM相交于E,设
=
,
=
,则向量
=( )
| AB |
| a |
| AC |
| b |
| AE |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
下面使用类比推理正确的是( )
| A、“若a•3=b•3,则a=b”类比推出“若a•0=b•0,则a=b” | ||||||||||||||
| B、“loga(xy)=logax+logay”类比推出“sin(α+β)=sinαsinβ” | ||||||||||||||
C、“(a+b)c=ac+bc”类比推出“(
| ||||||||||||||
| D、“(ab)n=anbn”类比推出“(a+b)n=an+bn” |
给出下列关系式:①a?{a,b};②a∈{a,b};③∅∈{a,b};④∅⊆{a};⑤{a}⊆{a,b};⑥{a}⊆{a}其中正确的是( )
| A、①②④⑤ | B、②③④⑤ |
| C、②④⑤ | D、②④⑤⑥ |
若幂函数y=(m2+3m-9)xm2-5的图象不过原点,则求m的值( )
| A、2 | B、-5 | C、2或-5 | D、-2 |
将正偶数按下表排成4列:

则2000在( )

则2000在( )
| A、第125行,第1列 |
| B、第125行,第2列 |
| C、第250行,第1列 |
| D、第250行,第4列 |
若α角的终边落在第三或第四象限,则
的终边落在( )
| α |
| 2 |
| A、第一或第三象限 |
| B、第二或第四象限 |
| C、第一或第四象限 |
| D、第三或第四象限 |